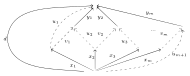
Isbell's zigzag theorem

Short description: Theorem of dominion in abstract algebra

Isbell's zigzag theorem, a theorem of abstract algebra characterizing the notion of a dominion, was introduced by American mathematician John R. Isbell in 1966. Dominion is a concept in semigroup theory, within the study of the properties of epimorphisms. For example, let U is a subsemigroup of S containing U, the inclusion map $U\hookrightarrow S$ is an epimorphism if and only if ${\mathrm{D}\mathrm{o}\mathrm{m}}_{\mathrm{S}}\mathrm{(}\mathrm{U}\mathrm{)}\mathrm{=}\mathrm{S}$, furthermore, a map $\alpha :S\to T$ is an epimorphism if and only if ${\mathrm{D}\mathrm{o}\mathrm{m}}_{\mathrm{T}}\mathrm{(}\mathrm{i}\mathrm{m}\mathrm{\alpha }\mathrm{)}\mathrm{=}\mathrm{T}$. The categories of rings and semigroups are examples of categories with non-surjective epimorphism, and the Zig-zag theorem gives necessary and sufficient conditions for determining whether or not a given morphism is epi. Proofs of this theorem are topological in nature, beginning with (Isbell 1966) for semigroups, and continuing by (Philip 1974), completing Isbell's original proof. The pure algebraic proofs were given by (Howie 1976) and (Storrer 1976).

Statement

Zig-zag

The dashed line is the spine of the zig-zag.

Zig-zag: If U is a submonoid of a monoid (or a subsemigroup of a semigroup) S, then a system of equalities;

$\begin{array}{rlrl}d& =x_1{u}_1,& u_1& =v_1{y}_1\\ x_{i-1}{v}_{i-1}& =x_i{u}_i,& u_i{y}_{i-1}& =v_i{y}_i(i=2,\dots ,m)\\ x_m{v}_m& =u_{m+1},& u_{m+1}{y}_m& =d\end{array}$

in which $u_1,\dots ,u_{m+1},v_1,\dots ,v_m\in U$ and $x_1,\dots ,x_m,y_1,\dots ,y_m\in S$, is called a zig-zag of length m in S over U with value d. By the spine of the zig-zag we mean the ordered (2m + 1)-tuple $(u_1,v_1,u_2,v_2,\dots ,u_m,v_m,u_{m+1})$.

Dominion

Dominion: Let U be a submonoid of a monoid (or a subsemigroup of a semigroup) S. The dominion ${\mathrm{D}\mathrm{o}\mathrm{m}}_{\mathrm{S}}\mathrm{(}\mathrm{U}\mathrm{)}$ is the set of all elements $s\in S$ such that, for all homomorphisms $f,g:S\to T$ coinciding on U, $f(s)=g(s)$.

We call a subsemigroup U of a semigroup U closed if ${\mathrm{D}\mathrm{o}\mathrm{m}}_{\mathrm{S}}\mathrm{(}\mathrm{U}\mathrm{)}\mathrm{=}\mathrm{U}$, and dense if ${\mathrm{D}\mathrm{o}\mathrm{m}}_{\mathrm{S}}\mathrm{(}\mathrm{U}\mathrm{)}\mathrm{=}\mathrm{S}$.

Isbell's zigzag theorem

Isbell's zigzag theorem:

If U is a submonoid of a monoid S then $d\in {\mathrm{D}\mathrm{o}\mathrm{m}}_{\mathrm{S}}\mathrm{(}\mathrm{U}\mathrm{)}$ if and only if either $d\in U$ or there exists a zig-zag in S over U with value d that is, there is a sequence of factorizations of d of the form

$d=x_1{u}_1=x_1{v}_1{y}_1=x_2{u}_2{y}_1=x_2{v}_2{y}_2=\cdots =x_m{v}_m{y}_m=u_{m+1}{y}_m$

This statement also holds for semigroups.

For monoids, this theorem can be written more concisely:

Let S be a monoid, let U be a submonoid of S, and let $d\in S$. Then $d\in {\mathrm{D}\mathrm{o}\mathrm{m}}_S(U)$ if and only if $d\otimes 1=1\otimes d$ in the tensor product $S{\otimes }_{U}S$.

Application

• Let U be a commutative subsemigroup of a semigroup S. Then ${\mathrm{D}\mathrm{o}\mathrm{m}}_{\mathrm{S}}\mathrm{(}\mathrm{U}\mathrm{)}$ is commutative.
• Every epimorphism $\alpha :S\to T$ from a finite commutative semigroup S to another semigroup T is surjective.
• Inverse semigroups are absolutely closed.
• Example of non-surjective epimorphism in the category of rings: The inclusion $i:(\mathbb{\mathbb{Z}},\cdot )\hookrightarrow (\mathbb{\mathbb{Q}},\cdot )$ is an epimorphism in the category of all rings and ring homomorphisms by proving that any pair of ring homomorphisms $\beta ,\gamma :\mathbb{\mathbb{Q}}\to \mathbb{ℝ}$ which agree on $\mathbb{\mathbb{Z}}$ are fact equal.

A proof sketch for example of non-surjective epimorphism in the category of rings by using zig-zag

We show that: Let $\beta ,\gamma$ to be ring homomorphisms, and $n,m\in \mathbb{\mathbb{Z}}$, $n\ne 0$. When $\beta (m)=\gamma (m)$ for all $m\in \mathbb{\mathbb{Z}}$, then $\beta \left(\frac{m}{n}\right)=\gamma \left(\frac{m}{n}\right)$ for all $\frac{m}{n}\in \mathbb{\mathbb{Q}}$.

$\begin{array}{rl}\beta \left(\frac{m}{n}\right)& =\beta (\frac{1}{n}\cdot m)=\beta \left(\frac{1}{n}\right)\cdot \beta (m)\\ & =\beta \left(\frac{1}{n}\right)\cdot \gamma (m)=\beta \left(\frac{1}{n}\right)\cdot \gamma (mn\cdot \frac{1}{n})\\ & =\beta \left(\frac{1}{n}\right)\cdot \gamma (mn)\cdot \gamma \left(\frac{1}{n}\right)=\beta \left(\frac{1}{n}\right)\cdot \beta (mn)\cdot \gamma \left(\frac{1}{n}\right)\\ & =\beta (\frac{1}{n}\cdot mn)\cdot \gamma \left(\frac{1}{n}\right)=\beta (m)\cdot \gamma \left(\frac{1}{n}\right)=\gamma (m)\cdot \gamma \left(\frac{1}{n}\right)\\ & =\gamma (m\cdot \frac{1}{n})=\gamma \left(\frac{m}{n}\right),\end{array}$

as required.

See also

• Epimorphisms

References

Bibliography

• Higgins, P. M. (1981). "Epis are onto for generalized inverse semigroups". Semigroup Forum 23: 255–260. doi:10.1007/BF02676649. http://eudml.org/doc/134518. Retrieved 2023-08-20. 
• Higgins, P. M. (1983). "The determination of all varieties consisting of absolutely closed semigroups". Proceedings of the American Mathematical Society 87 (3): 419–421. doi:10.1090/S0002-9939-1983-0684630-8. 
• Higgins, Peter M. (1986). "Completely semisimple semigroups and epimorphisms". Proceedings of the American Mathematical Society 96 (3): 387–390. doi:10.1090/S0002-9939-1986-0822424-3. 
• Higgins, Peter M. (1988). "Epimorphisms and amalgams". Colloquium Mathematicum 56: 1–17. doi:10.4064/cm-56-1-1-17. http://eudml.org/doc/266906. Retrieved 2023-07-29. 
• Higgins, Peter M. (1990). "A short proof of Isbell's zigzag theorem". Pacific Journal of Mathematics 144 (1): 47–50. doi:10.2140/pjm.1990.144.47. 
• Higgins, Peter M. (2016). "Ramsey's theorem in algebraic semigroup". First International Tainan-Moscow Algebra Workshop: Proceedings of the International Conference held at National Cheng Kung University Tainan, Taiwan, Republic of China, July 23–August 22, 1994. Walter de Gruyter GmbH & Co KG. ISBN 9783110883220. https://books.google.com/books?id=WZdsDwAAQBAJ&pg=PA24. Retrieved August 13, 2023. 
• Hall, T. E. (1982). "Epimorphisms and dominions". Semigroup Forum 24: 271–284. doi:10.1007/BF02572773. http://eudml.org/doc/134552. Retrieved 2023-08-10. 
• Hall, T. E.; Jones, P. R. (1983). "Epis are onto for finite regular semigroups". Proceedings of the Edinburgh Mathematical Society 26 (2): 151–162. doi:10.1017/S0013091500016850. 
• Isbell, John R. (1966). "Epimorphisms and Dominions". Proceedings of the Conference on Categorical Algebra. pp. 232–246. doi:10.1007/978-3-642-99902-4_9. ISBN 978-3-642-99904-8. https://books.google.com/books?id=rwX9CAAAQBAJ&pg=PA239. Retrieved 2023-07-26. 
• Howie, J.M; Isbell, J.R (1967). "Epimorphisms and dominions. II". Journal of Algebra 6: 7–21. doi:10.1016/0021-8693(67)90010-5. 
• Howie, John M. (1976). An introduction to semigroup theory. L.M.S. Monographs; 7. Academic Press. ISBN 9780123569509. 
• Howie, John M. (1996). "Isbell's zigzag theorem and its consequences". Semigroup Theory and its Applications. pp. 81–92. doi:10.1017/CBO9780511661877.007. ISBN 9780521576697. https://books.google.com/books?id=Hp1k-ROfeLEC&pg=PA81. Retrieved 2023-08-05. 
• Isbell, John R. (1969). "Epimorphisms and Dominions. IV". Journal of the London Mathematical Society: 265–273. doi:10.1112/jlms/s2-1.1.265. 
• Hoffman, Piotr (2008). "A Proof of Isbell's Zigzag Theorem". Journal of the Australian Mathematical Society 84 (2): 229–232. doi:10.1017/S1446788708000384. 
• Mitchell, Barry (1972). "The Dominion of Isbell". Transactions of the American Mathematical Society 167: 319–331. doi:10.1090/S0002-9947-1972-0294441-0. 
• Renshaw, James (2002). "On Free Products of Semigroups and a New Proof of Isbell's Zigzag Theorem". Journal of Algebra 251 (1): 12–15. doi:10.1006/jabr.2002.9143. 
• Stenström, Bo (1971). "Flatness and localization over monoids". Mathematische Nachrichten 48 (1–6): 315–334. doi:10.1002/mana.19710480124. 
• Storrer, H. (1976). "An algebraic proof of Isbell' s zigzag theorem". Semigroup Forum 12: 83–88. doi:10.1007/BF02195912. http://eudml.org/doc/134160. Retrieved 2023-07-31. 

Further reading

• Alam, Noor; Higgins, Peter M.; Khan, Noor Mohammad (2020). "Epimorphisms, dominions and ${\mathscr{H}}$-commutative semigroups". Semigroup Forum 100 (2): 349–363. doi:10.1007/s00233-019-10050-z. 
• Ahanger, Shabir Ahmad; Shah, Aftab Hussain (2020). "Epimorphisms, dominions and varieties of bands". Semigroup Forum 100 (3): 641–650. doi:10.1007/s00233-019-10047-8. 
• Khan, N. M. (1985). "On saturated permutative varieties and consequences of permutation identities". Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics 38 (2): 186–197. doi:10.1017/S1446788700023041. 
• Isbell, John R. (1968). "Epimorphisms and Dominions, III". American Journal of Mathematics 90 (4): 1025–1030. doi:10.2307/2373286. https://www.jstor.org/stable/2373286. 
• Isbell, J. R. (1973). "Epimorphisms and dominions, V". Algebra Universalis 3 (1): 318–320. doi:10.1007/BF02945133. 
• Scheiblich, E. (1976). "On epics and dominions of bands". Semigroup Forum 13 (1): 103–114. doi:10.1007/BF02194926. http://eudml.org/doc/134201. 
• Philip, J.M (1974). "A proof of Isbell's zig-zag theorem". Journal of Algebra 32 (2): 328–331. doi:10.1016/0021-8693(74)90141-0. 
• Higgins, Peter M. (1985). "Epimorphisms, dominions and semigroups". Algebra Universalis 21 (2–3): 225–233. doi:10.1007/BF01188058. 
• Higgins, Peter M. (1992). Techniques of Semigroup Theory. Oxford University Press. ISBN 9780198535775. 
• Howie, John M. (1995). "Semigroup amalgams". Fundamentals of Semigroup Theory. Clarendon Press. ISBN 0-19-851194-9. 
• Campercholi, Miguel (2018). "Dominions and Primitive Positive Functions". The Journal of Symbolic Logic 83 (1): 40–54. doi:10.1017/jsl.2017.18. 

External links

• Nicol, Andrew W.. "WHAT IS... THE ZIGZAG THEOREM?". https://math.osu.edu/sites/math.osu.edu/files/ZigZag.pdf.