Isbell duality

Short description: Adjunction between a category of co/presheaf under the co/Yoneda embedding

In mathematics, Isbell conjugacy (a.k.a. Isbell duality or Isbell adjunction) (named after John R. Isbell) is a fundamental construction of enriched category theory formally introduced by William Lawvere in 1986. That is a duality between covariant and contravariant representable presheaves associated with an objects of categories under the Yoneda embedding. In addition, Lawvere is states as follows; "Then the conjugacies are the first step toward expressing the duality between space and quantity fundamental to mathematics".

Definition

Yoneda embedding

The (covariant) Yoneda embedding is a covariant functor from a small category ${𝒜}$ into the category of presheaves $[{{𝒜}}^{op},{𝒱}]$ on ${𝒜}$, taking $X\in {𝒜}$ to the contravariant representable functor:

$Y(h^{\bullet }):{𝒜}\to [{{𝒜}}^{op},{𝒱}]$

$X\mapsto \mathrm{h}\mathrm{o}\mathrm{m}(-,X).$

and the co-Yoneda embedding (a.k.a. dual Yoneda embedding) is a contravariant functor from a small category ${𝒜}$ into the opposite of the category of co-presheaves ${[{𝒜},{𝒱}]}^{op}$ on ${𝒜}$, taking $X\in {𝒜}$ to the covariant representable functor:

$Z({h_{\bullet }}^{op}):{𝒜}\to {[{𝒜},{𝒱}]}^{op}$

$X\mapsto \mathrm{h}\mathrm{o}\mathrm{m}(X,-).$

Isbell duality

Origin of symbols ${𝒪}$ (“ring of functions”) and $\mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}$ (“spectrum”): (Lawvere 1986) says that; "${𝒪}$" assigns to each general space the algebra of functions on it, whereas "$\mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}$" assigns to each algebra its “spectrum” which is a general space.

note:In order for this commutative diagram to hold, it is required that ${𝒜}$ is small and E is co-complete.

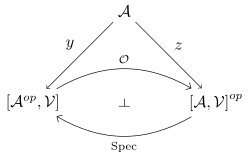
Every functor $F:{{𝒜}}^{\mathrm{o}\mathrm{p}}\to {𝒱}$ has an Isbell conjugate of a functor $F^{\ast }:{𝒜}\to {𝒱}$, given by

$F^{\ast }(X)=\mathrm{h}\mathrm{o}\mathrm{m}(F,y(X)).$

In contrast, every functor $G:{𝒜}\to {𝒱}$ has an Isbell conjugate of a functor $G^{\ast }:{{𝒜}}^{\mathrm{o}\mathrm{p}}\to {𝒱}$ given by

$G^{\ast }(X)=\mathrm{h}\mathrm{o}\mathrm{m}(z(X),G).$

These two functors are not typically inverses, or even natural isomorphisms. Isbell duality asserts that the relationship between these two functors is an adjunction.

Isbell duality is the relationship between Yoneda embedding and co-Yoneda embedding；

Let ${𝒱}$ be a symmetric monoidal closed category, and let ${𝒜}$ be a small category enriched in ${𝒱}$.

The Isbell duality is an adjunction between the functor categories; $({𝒪}⊣\mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}):[{{𝒜}}^{op},{𝒱}]\underset{\mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}}{\stackrel{{𝒪}}{\rightleftarrows }}{[{𝒜},{𝒱}]}^{op}$.

Applying the nerve construction, the functors ${𝒪}⊣\mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}$ of Isbell duality are such that ${𝒪}\cong \mathrm{L}\mathrm{a}{\mathrm{n}}_{\mathrm{Y}}\mathrm{Z}$ and $\mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}\cong \mathrm{L}\mathrm{a}{\mathrm{n}}_{\mathrm{Z}}\mathrm{Y}$.

See also

• Kan extension
• Limit (category theory)
• Isbell completion
• Profunctor

Bibliography

• Avery, Tom; Leinster, Tom (2021), "Isbell conjugacy and the reflexive completion", Theory and Applications of Categories 36: 306–347, doi:10.70930/tac/r1jknjot, http://www.tac.mta.ca/tac/volumes/36/12/36-12.pdf 
• Awodey, Steve (2006), Category Theory, doi:10.1093/acprof:oso/9780198568612.001.0001, ISBN 978-0-19-856861-2 
• Baez, John C. (2022), "Isbell Duality", Notices Amer. Math. Soc. 70: 140–141, doi:10.1090/noti2602, https://www.ams.org/journals/notices/202301/noti2602/noti2602.html?adat=January%202023&trk=2602&galt=none&cat=column&pdfissue=202301&pdffile=rnoti-p140.pdf 

Barr, Michael; Kennison, John F.; Raphael, R. (2009), "Isbell duality for modules", Theory and Applications of Categories 22: 401–419, doi:10.70930/tac/1zcfxg2x 

• Day, Brian J.; Lack, Stephen (2007), "Limits of small functors", Journal of Pure and Applied Algebra 210 (3): 651–663, doi:10.1016/j.jpaa.2006.10.019 .
• Di Liberti, Ivan (2020), "Codensity: Isbell duality, pro-objects, compactness and accessibility", Journal of Pure and Applied Algebra 224 (10), doi:10.1016/j.jpaa.2020.106379 
• Fosco, Loregian (22 July 2021), (Co)end Calculus, Cambridge University Press, doi:10.1017/9781108778657, ISBN 9781108746120, https://books.google.com/books?id=cfIuEAAAQBAJ&dq&pg=PA90 
• Gutierres, Gonçalo; Hofmann, Dirk (2013), "Approaching Metric Domains", Applied Categorical Structures 21 (6): 617–650, doi:10.1007/s10485-011-9274-z 
• Shen, Lili; Zhang, Dexue (2013), "Categories enriched over a quantaloid: Isbell adjunctions and Kan adjunctions", Theory and Applications of Categories 28 (20): 577–615, doi:10.70930/tac/6l0334s5, http://www.tac.mta.ca/tac/volumes/28/20/28-20.pdf 
• Isbell, J. R. (1960), "Adequate subcategories", Illinois Journal of Mathematics 4 (4), doi:10.1215/ijm/1255456274 
• Isbell, John R. (1966), "Structure of categories", Bulletin of the American Mathematical Society 72 (4): 619–656, doi:10.1090/S0002-9904-1966-11541-0 
• Imamura, Yuki (2022), "Grothendieck Enriched Categories", Applied Categorical Structures 30 (5): 1017–1041, doi:10.1007/s10485-022-09681-1 
• Kelly, Gregory Maxwell (1982), Basic concepts of enriched category theory, London Mathematical Society Lecture Note Series, 64, Cambridge University Press, Cambridge-New York, ISBN 0-521-28702-2, http://www.tac.mta.ca/tac/reprints/articles/10/tr10.pdf 
• "Taking categories seriously", Revista Colombiana de Matemáticas 20 (3–4): 147–178, 1986, http://eudml.org/doc/181771 
  • "Taking categories seriously", Reprints in Theory and Applications of Categories (8): 1–24, 2005, http://www.tac.mta.ca/tac/reprints/articles/8/tr8.pdf 
• Lawvere, F. William (February 2016), "Birkhoff's Theorem from a geometric perspective: A simple example", Categories and General Algebraic Structures with Applications 4 (1): 1–8, https://cgasa.sbu.ac.ir/article_12425_1874.html 
• Melliès, Paul-André; Zeilberger, Noam (2018), "An Isbell duality theorem for type refinement systems", Mathematical Structures in Computer Science 28 (6): 736–774, doi:10.1017/S0960129517000068 
• Pratt, Vaughan (1996), "Broadening the denotational semantics of linear logic", Electronic Notes in Theoretical Computer Science 3: 155–166, doi:10.1016/S1571-0661(05)80415-3 
• Rutten, J.J.M.M. (1998), "Weighted colimits and formal balls in generalized metric spaces", Topology and Its Applications 89 (1–2): 179–202, doi:10.1016/S0166-8641(97)00224-1 
• Sturtz, Kirk (2018), "The factorization of the Giry monad", Advances in Mathematics 340: 76–105, doi:10.1016/j.aim.2018.10.007 
  • Sturtz, K. (2019), "Erratum and Addendum: The factorization of the Giry monad", arXiv:1907.00372 [math.CT]
• Wood, R.J (1982), "Some remarks on total categories", Journal of Algebra 75 (2): 538–545, doi:10.1016/0021-8693(82)90055-2 
• Willerton, Simon (2013), "Tight spans, Isbell completions and semi-tropical modules", Theory and Applications of Categories 28 (22): 696–732, doi:10.70930/tac/rkp3zgxc, http://www.tac.mta.ca/tac/volumes/28/22/28-22.pdf 

External links

• Di Liberti, Ivan; Loregian, Fosco (2019), "On the unicity of formal category theories", arXiv:1901.01594 [math.CT]
• Loregian, Fosco (2018), Kan extensions, https://tetrapharmakon.github.io/stuff/REFCARDS_kan.pdf 
• Valence, Arnaud (2017), Esquisse d'une dualité géométrico-algébrique multidisciplinaire : la dualité d'Isbell, Thèse en cotutelle en Philosophie – Étude des Systèmes, soutenue le 30 mai 2017., https://scd-resnum.univ-lyon3.fr/out/theses/2017_out_valence_a.pdf 
• Isbell duality, https://ncatlab.org/nlab/show/Isbell+duality 
• space and quantity, https://ncatlab.org/nlab/show/space+and+quantity##Isbell 
• Yoneda embedding, https://ncatlab.org/nlab/show/Yoneda+embedding 
• co-Yoneda lemma, https://ncatlab.org/nlab/show/co-Yoneda+lemma 
• copresheaf, https://ncatlab.org/nlab/show/copresheaf 
• Natural transformations and presheaves: Remark 1.28. (presheaves as generalized spaces), https://ncatlab.org/nlab/show/geometry+of+physics+–+basic+notions+of+category+theory#NaturalTransformationsAndPresheaves 
• Opposite functors, https://ncatlab.org/nlab/show/opposite+category#opposite_functors