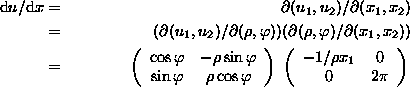Jacobi determinant

Let

be a function of n variables, and let

be a function of x, where inversely x can be expressed as a function of u,

The formula for a change of variable in an n-dimensional integral is then

is an integration region, and one integrates over all , or equivalently, all . is the Jacobi matrix and

is the absolute value of the Jacobi determinant or Jacobian.

As an example, take n=2 and

Define

Then by the chain rule ( Jacobi Matrix)

The Jacobi determinant is

and

This shows that if x₁ and x₂ are independent random variables with uniform distributions between 0 and 1, then u₁ and u₂ as defined above are independent random variables with standard normal distributions ( Transformation of Random Variables).