King's graph

From HandWiki
Short description: Graph that represents all legal moves of the king on a chessboard
King's graph
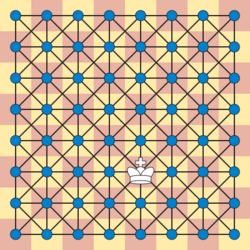8×8 king's graph
Verticesnm
Edges4nm−3(n+m)+2
Girth3 when min⁡(m,n)>1
Chromatic number4 when min⁡(m,n)>1
Chromatic index8 when min⁡(m,n)>2
Table of graphs and parameters

In graph theory, a king's graph is a graph that represents all legal moves of the king chess piece on a chessboard where each vertex represents a square on a chessboard and each edge is a legal move. More specifically, an n×m king's graph is a king's graph of an n×m chessboard.[1] It is the map graph formed from the squares of a chessboard by making a vertex for each square and an edge for each two squares that share an edge or a corner. It can also be constructed as the strong product of two path graphs.[2]

For an n×m king's graph the total number of vertices is nm and the number of edges is 4nm−3(n+m)+2. For a square n×n king's graph this simplifies so that the total number of vertices is n2 and the total number of edges is (2n−2)(2n−1).[3]

The neighbourhood of a vertex in the king's graph corresponds to the Moore neighborhood for cellular automata.[4] A generalization of the king's graph, called a kinggraph, is formed from a squaregraph (a planar graph in which each bounded face is a quadrilateral and each interior vertex has at least four neighbors) by adding the two diagonals of every quadrilateral face of the squaregraph.[5]

In the drawing of a king's graph obtained from an n×m chessboard, there are (n−1)(m−1) crossings, but it is possible to obtain a drawing with fewer crossings by connecting the two nearest neighbors of each corner square by a curve outside the chessboard instead of by a diagonal line segment. In this way, (n−1)(m−1)−4 crossings are always possible. For the king's graph of small chessboards, other drawings lead to even fewer crossings; in particular every 2×n king's graph is a planar graph. However, when both n and m are at least four, and they are not both equal to four, (n−1)(m−1)−4 is the optimal number of crossings.[6][7]

See also

References

  1. ↑ Chang, Gerard J. (1998), "Algorithmic aspects of domination in graphs", in Du, Ding-Zhu; Pardalos, Panos M., Handbook of combinatorial optimization, Vol. 3, Boston, MA: Kluwer Acad. Publ., pp. 339–405 . Chang defines the king's graph on p. 341.
  2. ↑ Berend, Daniel; Korach, Ephraim; Zucker, Shira (2005), "Two-anticoloring of planar and related graphs", 2005 International Conference on Analysis of Algorithms, Discrete Mathematics & Theoretical Computer Science Proceedings, Nancy: Association for Discrete Mathematics & Theoretical Computer Science, pp. 335–341, http://www.emis.de/journals/DMTCS/pdfpapers/dmAD0130.pdf .
  3. ↑ Sloane, N. J. A., ed. "Sequence A002943". OEIS Foundation. https://oeis.org/A002943. 
  4. ↑ "Two-dimensional formal languages and pattern recognition by cellular automata", 12th Annual Symposium on Switching and Automata Theory, 1971, pp. 144–152, doi:10.1109/SWAT.1971.29 .
  5. ↑ Chepoi, Victor; Dragan, Feodor; Vaxès, Yann (2002), "Center and diameter problems in plane triangulations and quadrangulations", Proceedings of the Thirteenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '02), pp. 346–355, ISBN 0-89871-513-X, https://archive.org/details/proceedingsofthi2002acms/page/346 .
  6. ↑ Klešč, Marián; Petrillová, Jana; Valo, Matúš (2013), "Minimal number of crossings in strong product of paths", Carpathian Journal of Mathematics 29 (1): 27–32, doi:10.37193/CJM.2013.01.13 
  7. ↑ Ma, Dengju (2017), "The crossing number of the strong product of two paths", The Australasian Journal of Combinatorics 68: 35–47, https://ajc.maths.uq.edu.au/pdf/68/ajc_v68_p035.pdf 



Retrieved from "https://handwiki.org/wiki/index.php?title=King%27s_graph&oldid=242714"