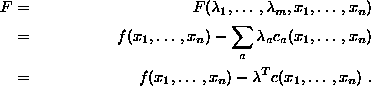Lagrange multipliers
Let ![]() be a function of n variables
be a function of n variables ![]() . If the n variables are independent, then a local minimum of f can be found by solving the n equations
. If the n variables are independent, then a local minimum of f can be found by solving the n equations
In general, these equations define an extremum of f (a minimum, maximum or saddle point).
If the n variables are not independent, but satisfy m constraint equations
gradient of f need not vanish at the extremum, it need only be orthogonal to the (n-m)-dimensional surface described by the constraint equations. That is,
or in matrix notation ![]() , where the coefficients
, where the coefficients ![]() are called Lagrange multipliers. The above equations together may be written as
are called Lagrange multipliers. The above equations together may be written as
where
A useful method for solving these equations is the Newton-Raphson method. Stick to matrix notation and let
i.e. ![]() Hessian of f and
Hessian of f and ![]() (
( ![]() Jacobi Matrix). Assuming that x is an approximation to the required solution, a better approximation
Jacobi Matrix). Assuming that x is an approximation to the required solution, a better approximation ![]() is calculated. This procedure is iterated until some convergence criterion is satisfied, e.g. until the equations are satisfied to a given precision, or until the step
is calculated. This procedure is iterated until some convergence criterion is satisfied, e.g. until the equations are satisfied to a given precision, or until the step ![]() is ``sufficiently small.
is ``sufficiently small.
For the unconstrained minimization problem, the Newton-Raphson formula is
For the constrained problem, the Newton-Raphson formula becomes
where the superscripts `u' or `c' stand for ``unconstrained or ``constrained.
Apart from the additional term in the formula for ![]() , there is no change in the procedure.
, there is no change in the procedure.
Note in particular that the first guess for the solution may well violate the constraint equations, since these equations are solved during the iteration procedure.
Note also that if efficiency is essential, ![]() and
and ![]() can be calculated without explicit inversions of the matrices involved. For example, the
can be calculated without explicit inversions of the matrices involved. For example, the ![]() matrix
matrix ![]() should be calculated by solution of the linear equation
should be calculated by solution of the linear equation ![]() , not by calculation of A-1.
, not by calculation of A-1.
The formulae given here for ![]() and
and ![]() are only valid if the matrix A has an inverse. If A is singular, then one must solve the linear equations
are only valid if the matrix A has an inverse. If A is singular, then one must solve the linear equations
The Lagrange multiplier method is in general very easy to use. It may, however, be more sensitive to rounding errors and also more time-consuming than the elimination method ( ![]() Constraints), in which the constraint equations are solved explicitly. However, an explicit solution is frequently not possible. also Minimization.
Constraints), in which the constraint equations are solved explicitly. However, an explicit solution is frequently not possible. also Minimization.