Lamé's special quartic
From HandWiki
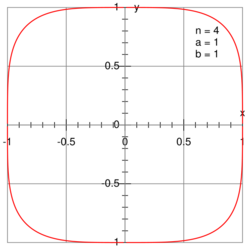
Lamé's special quartic, named after Gabriel Lamé, is the graph of the equation
- [math]\displaystyle{ x^4 + y^4 = r^4 }[/math]
where [math]\displaystyle{ r \gt 0 }[/math].[1] It looks like a rounded square with "sides" of length [math]\displaystyle{ 2r }[/math] and centered on the origin. This curve is a squircle centered on the origin, and it is a special case of a superellipse.[2]
Because of Pierre de Fermat's only surviving proof, that of the n = 4 case of Fermat's Last Theorem, if r is rational there is no non-trivial rational point (x, y) on this curve (that is, no point for which both x and y are non-zero rational numbers).
References
- ↑ Oakley, Cletus Odia (1958), Analytic Geometry Problems, College Outline Series, 108, Barnes & Noble, p. 171.
- ↑ Schwartzman, Steven (1994), The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English, MAA Spectrum, Mathematical Association of America, p. 212, ISBN 9780883855119, https://books.google.com/books?id=SRw4PevE4zUC&pg=PA212.
 |  |
