Leavitt path algebra

In mathematics, a Leavitt path algebra is a universal algebra constructed from a directed graph. Leavitt path algebras generalize Leavitt algebras and may be considered as algebraic analogues of graph C*-algebras.

History

Leavitt path algebras were simultaneously introduced in 2005 by Gene Abrams and Gonzalo Aranda Pino as well as by Pere Ara, María Moreno, and Enrique Pardo, with neither of the two groups aware of the other's work. Leavitt path algebras have been investigated by dozens of mathematicians since their introduction, and in 2020 Leavitt path algebras were added to the Mathematics Subject Classification with code 16S88 under the general discipline of Associative Rings and Algebras.

The basic reference is the book Leavitt Path Algebras.

Graph terminology

The theory of Leavitt path algebras uses terminology for graphs similar to that of C*-algebraists, which differs slightly from that used by graph theorists. The term graph is typically taken to mean a directed graph [math]\displaystyle{ E=(E^0, E^1, r, s) }[/math] consisting of a countable set of vertices [math]\displaystyle{ E^0 }[/math], a countable set of edges [math]\displaystyle{ E^1 }[/math], and maps [math]\displaystyle{ r, s : E^1 \rightarrow E^0 }[/math] identifying the range and source of each edge, respectively. A vertex [math]\displaystyle{ v \in E^0 }[/math] is called a sink when [math]\displaystyle{ s^{-1}(v) = \emptyset }[/math]; i.e., there are no edges in [math]\displaystyle{ E }[/math] with source [math]\displaystyle{ v }[/math]. A vertex [math]\displaystyle{ v \in E^0 }[/math] is called an infinite emitter when [math]\displaystyle{ s^{-1}(v) }[/math] is infinite; i.e., there are infinitely many edges in [math]\displaystyle{ E }[/math] with source [math]\displaystyle{ v }[/math]. A vertex is called a singular vertex if it is either a sink or an infinite emitter, and a vertex is called a regular vertex if it is not a singular vertex. Note that a vertex [math]\displaystyle{ v }[/math] is regular if and only if the number of edges in [math]\displaystyle{ E }[/math] with source [math]\displaystyle{ v }[/math] is finite and nonzero. A graph is called row-finite if it has no infinite emitters; i.e., if every vertex is either a regular vertex or a sink.

A path is a finite sequence of edges [math]\displaystyle{ e_1 e_2 \ldots e_n }[/math] with [math]\displaystyle{ r(e_i) = s(e_{i+1}) }[/math] for all [math]\displaystyle{ 1 \leq i \leq n-1 }[/math]. An infinite path is a countably infinite sequence of edges [math]\displaystyle{ e_1 e_2 \ldots }[/math] with [math]\displaystyle{ r(e_i) = s(e_{i+1}) }[/math] for all [math]\displaystyle{ i \in \mathbb{N} }[/math]. A cycle is a path [math]\displaystyle{ e_1 e_2 \ldots e_n }[/math] with [math]\displaystyle{ r(e_n) = s(e_1) }[/math], and an exit for a cycle [math]\displaystyle{ e_1 e_2 \ldots e_n }[/math] is an edge [math]\displaystyle{ f \in E^1 }[/math] such that [math]\displaystyle{ s(f) = s(e_i) }[/math] and [math]\displaystyle{ f \neq e_i }[/math] for some [math]\displaystyle{ 1 \leq i \leq n }[/math]. A cycle [math]\displaystyle{ e_1 e_2 \ldots e_n }[/math] is called a simple cycle if [math]\displaystyle{ s(e_i) \neq s(e_1) }[/math] for all [math]\displaystyle{ 2 \leq i \leq n }[/math].

The following are two important graph conditions that arise in the study of Leavitt path algebras.

Condition (L): Every cycle in the graph has an exit.

Condition (K): There is no vertex in the graph that is on exactly one simple cycle. Equivalently, a graph satisfies Condition (K) if and only if each vertex in the graph is either on no cycles or on two or more simple cycles.

The Cuntz–Krieger relations and the universal property

Fix a field [math]\displaystyle{ K }[/math]. A Cuntz–Krieger [math]\displaystyle{ E }[/math]-family is a collection [math]\displaystyle{ \{ s_e^*, s_e, p_v : e \in E^1, v \in E^0 \} }[/math] in a [math]\displaystyle{ K }[/math]-algebra such that the following three relations (called the Cuntz–Krieger relations) are satisfied:

(CK0) [math]\displaystyle{ p_v p_w = \begin{cases} p_v & \text{if } v=w \\ 0 & \text{if } v\neq w \end{cases} \quad }[/math] for all [math]\displaystyle{ v, w \in E^0 }[/math],

(CK1) [math]\displaystyle{ s_e^* s_f = \begin{cases} p_{r(e)} & \text{if } e=f \\ 0 & \text{if } e\neq f \end{cases} \quad }[/math] for all [math]\displaystyle{ e, f \in E^0 }[/math],

(CK2) [math]\displaystyle{ p_v = \sum_{s(e)=v} s_e s_e^* }[/math] whenever [math]\displaystyle{ v }[/math] is a regular vertex, and

(CK3) [math]\displaystyle{ p_{s(e)} s_e = s_e }[/math] for all [math]\displaystyle{ e \in E^1 }[/math].

The Leavitt path algebra corresponding to [math]\displaystyle{ E }[/math], denoted by [math]\displaystyle{ L_K(E) }[/math], is defined to be the [math]\displaystyle{ K }[/math]-algebra generated by a Cuntz–Krieger [math]\displaystyle{ E }[/math]-family that is universal in the sense that whenever [math]\displaystyle{ \{ t_e, t_e^*, q_v : e \in E^1, v \in E^0 \} }[/math] is a Cuntz–Krieger [math]\displaystyle{ E }[/math]-family in a [math]\displaystyle{ K }[/math]-algebra [math]\displaystyle{ A }[/math] there exists a [math]\displaystyle{ K }[/math]-algebra homomorphism [math]\displaystyle{ \phi : L_K(E) \to A }[/math] with [math]\displaystyle{ \phi(s_e) = t_e }[/math] for all [math]\displaystyle{ e \in E^1 }[/math], [math]\displaystyle{ \phi(s_e^*) = t_e^* }[/math] for all [math]\displaystyle{ e \in E^1 }[/math], and [math]\displaystyle{ \phi(p_v)=q_v }[/math] for all [math]\displaystyle{ v \in E^0 }[/math].

We define [math]\displaystyle{ p_v^* := p_v }[/math] for [math]\displaystyle{ v \in E^0 }[/math], and for a path [math]\displaystyle{ \alpha := e_1 \ldots e_n }[/math] we define [math]\displaystyle{ s_\alpha := s_{e_1} \ldots s_{e_n} }[/math] and [math]\displaystyle{ s_\alpha^* := s_{e_n}^* \ldots s_{e_1}^* }[/math]. Using the Cuntz–Krieger relations, one can show that

[math]\displaystyle{ L_K(E) = \operatorname{span}_K \{ s_\alpha s_\beta^* : \alpha \text{ and } \beta \text{ are paths in } E \}. }[/math]

Thus a typical element of [math]\displaystyle{ L_K(E) }[/math] has the form [math]\displaystyle{ \sum_{i=1}^n \lambda_i s_{\alpha_i} s_{\beta_i}^* }[/math] for scalars [math]\displaystyle{ \lambda_1, \ldots,\lambda_n \in K }[/math] and paths [math]\displaystyle{ \alpha_1, \ldots, \alpha_n, \beta_1, \ldots, \beta_n }[/math] in [math]\displaystyle{ E }[/math]. If [math]\displaystyle{ K }[/math] is a field with an involution [math]\displaystyle{ \lambda \mapsto \overline{\lambda} }[/math] (e.g., when [math]\displaystyle{ K=\mathbb{C} }[/math]), then one can define a *-operation on [math]\displaystyle{ L_K(E) }[/math] by [math]\displaystyle{ \sum_{i=1}^n \lambda_i s_{\alpha_i} s_{\beta_i}^* \mapsto \sum_{i=1}^n \overline{\lambda_i} s_{\beta_i} s_{\alpha_i}^* }[/math] that makes [math]\displaystyle{ L_K(E) }[/math] into a *-algebra.

Moreover, one can show that for any graph [math]\displaystyle{ E }[/math], the Leavitt path algebra [math]\displaystyle{ L_{\mathbb{C}}(E) }[/math] is isomorphic to a dense *-subalgebra of the graph C*-algebra [math]\displaystyle{ C^*(E) }[/math].

Examples

Leavitt path algebras has been computed for many graphs, and the following table shows some particular graphs and their Leavitt path algebras. We use the convention that a double arrow drawn from one vertex to another and labeled [math]\displaystyle{ \infty }[/math] indicates that there are a countably infinite number of edges from the first vertex to the second.

Directed graph [math]\displaystyle{ E }[/math]	Leavitt path algebra [math]\displaystyle{ L_K(E) }[/math]
	[math]\displaystyle{ K }[/math], the underlying field
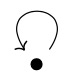	[math]\displaystyle{ K[x,x^{-1}] }[/math], the Laurent polynomials with coefficients in [math]\displaystyle{ K }[/math]
	[math]\displaystyle{ M_n(K) }[/math], the [math]\displaystyle{ n \times n }[/math] matrices with entries in [math]\displaystyle{ K }[/math]
	[math]\displaystyle{ M_\infty {K} }[/math], the countably indexed, finitely supported matrices with entries in [math]\displaystyle{ K }[/math]
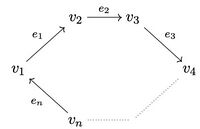	[math]\displaystyle{ M_n(K[x,x^{-1}]) }[/math], the [math]\displaystyle{ n \times n }[/math] matrices with entries in [math]\displaystyle{ K[x,x^{-1}] }[/math]
	the Leavitt algebra [math]\displaystyle{ L_K(n) }[/math]
	[math]\displaystyle{ M_\infty {K}^1 }[/math], the unitization of the algebra [math]\displaystyle{ M_\infty {K} }[/math]

Correspondence between graph and algebraic properties

As with graph C*-algebras, graph-theoretic properties of [math]\displaystyle{ E }[/math] correspond to algebraic properties of [math]\displaystyle{ L_K(E) }[/math]. Interestingly, it is often the case that the graph properties of [math]\displaystyle{ E }[/math] that are equivalent to an algebraic property of [math]\displaystyle{ L_K(E) }[/math] are the same graph properties of [math]\displaystyle{ E }[/math] that are equivalent to corresponding C*-algebraic property of [math]\displaystyle{ C^*(E) }[/math], and moreover, many of the properties for [math]\displaystyle{ L_K(E) }[/math] are independent of the field [math]\displaystyle{ K }[/math].

The following table provides a short list of some of the more well-known equivalences. The reader may wish to compare this table with the corresponding table for graph C*-algebras.

Property of [math]\displaystyle{ E }[/math]	Property of [math]\displaystyle{ L_K(E) }[/math]
[math]\displaystyle{ E }[/math] is a finite, acylic graph.	[math]\displaystyle{ L_K(E) }[/math] is finite dimensional.
The vertex set [math]\displaystyle{ E^0 }[/math] is finite.	[math]\displaystyle{ L_K(E) }[/math] is unital (i.e., [math]\displaystyle{ L_K(E) }[/math] contains a multiplicative identity).
[math]\displaystyle{ E }[/math] has no cycles.	[math]\displaystyle{ L_K(E) }[/math] is an ultramatrical [math]\displaystyle{ K }[/math]-algebra (i.e., a direct limit of finite-dimensional [math]\displaystyle{ K }[/math]-algebras).
[math]\displaystyle{ E }[/math] satisfies the following three properties: Condition (L), for each vertex [math]\displaystyle{ v }[/math] and each infinite path [math]\displaystyle{ \alpha }[/math] there exists a directed path from [math]\displaystyle{ v }[/math] to a vertex on [math]\displaystyle{ \alpha }[/math], and for each vertex [math]\displaystyle{ v }[/math] and each singular vertex [math]\displaystyle{ w }[/math] there exists a directed path from [math]\displaystyle{ v }[/math] to [math]\displaystyle{ w }[/math]	[math]\displaystyle{ L_K(E) }[/math] is simple.
[math]\displaystyle{ E }[/math] satisfies the following three properties: Condition (L), for each vertex [math]\displaystyle{ v }[/math] in [math]\displaystyle{ E }[/math] there is a path from [math]\displaystyle{ v }[/math] to a cycle.	Every left ideal of [math]\displaystyle{ L_K(E) }[/math] contains an infinite idempotent. (When [math]\displaystyle{ L_K(E) }[/math] is simple this is equivalent to [math]\displaystyle{ L_K(E) }[/math] being a purely infinite ring.)

The grading

For a path [math]\displaystyle{ \alpha := e_1 \ldots e_n }[/math] we let [math]\displaystyle{ |\alpha| := n }[/math] denote the length of [math]\displaystyle{ \alpha }[/math]. For each integer [math]\displaystyle{ n \in \mathbb{Z} }[/math] we define [math]\displaystyle{ L_K(E)_n := \operatorname{span}_K \{ s_\alpha s_\beta^* : |\alpha|-|\beta| = n \} }[/math]. One can show that this defines a [math]\displaystyle{ \mathbb{Z} }[/math]-grading on the Leavitt path algebra [math]\displaystyle{ L_K(E) }[/math] and that [math]\displaystyle{ L_K(E) = \bigoplus_{n \in \mathbb{Z}} L_K(E)_n }[/math] with [math]\displaystyle{ L_K(E)_n }[/math] being the component of homogeneous elements of degree [math]\displaystyle{ n }[/math]. It is important to note that the grading depends on the choice of the generating Cuntz-Krieger [math]\displaystyle{ E }[/math]-family [math]\displaystyle{ \{ s_e, s_e^*, p_v : e \in E^1, v \in E^0 \} }[/math]. The grading on the Leavitt path algebra [math]\displaystyle{ L_K(E) }[/math] is the algebraic analogue of the gauge action on the graph C*-algebra [math]\displaystyle{ C*(E) }[/math], and it is a fundamental tool in analyzing the structure of [math]\displaystyle{ L_K(E) }[/math].

The uniqueness theorems

There are two well-known uniqueness theorems for Leavitt path algebras: the graded uniqueness theorem and the Cuntz-Krieger uniqueness theorem. These are analogous, respectively, to the gauge-invariant uniqueness theorem and Cuntz-Krieger uniqueness theorem for graph C*-algebras. Formal statements of the uniqueness theorems are as follows:

The Graded Uniqueness Theorem: Fix a field [math]\displaystyle{ K }[/math]. Let [math]\displaystyle{ E }[/math] be a graph, and let [math]\displaystyle{ L_K(E) }[/math] be the associated Leavitt path algebra. If [math]\displaystyle{ A }[/math] is a graded [math]\displaystyle{ K }[/math]-algebra and [math]\displaystyle{ \phi : L_K(E) \to A }[/math] is a graded algebra homomorphism with [math]\displaystyle{ \phi(p_v) \neq 0 }[/math] for all [math]\displaystyle{ v \in E^0 }[/math], then [math]\displaystyle{ \phi }[/math] is injective.

The Cuntz-Krieger Uniqueness Theorem: Fix a field [math]\displaystyle{ K }[/math]. Let [math]\displaystyle{ E }[/math] be a graph satisfying Condition (L), and let [math]\displaystyle{ L_K(E) }[/math] be the associated Leavitt path algebra. If [math]\displaystyle{ A }[/math] is a [math]\displaystyle{ K }[/math]-algebra and [math]\displaystyle{ \phi : L_K(E) \to A }[/math] is an algebra homomorphism with [math]\displaystyle{ \phi(p_v) \neq 0 }[/math] for all [math]\displaystyle{ v \in E^0 }[/math], then [math]\displaystyle{ \phi }[/math] is injective.

Ideal structure

We use the term ideal to mean "two-sided ideal" in our Leavitt path algebras. The ideal structure of [math]\displaystyle{ L_K(E) }[/math] can be determined from [math]\displaystyle{ E }[/math]. A subset of vertices [math]\displaystyle{ H \subseteq E^0 }[/math] is called hereditary if for all [math]\displaystyle{ e \in E^1 }[/math], [math]\displaystyle{ s(e) \in H }[/math] implies [math]\displaystyle{ r(e) \in H }[/math]. A hereditary subset [math]\displaystyle{ H }[/math] is called saturated if whenever [math]\displaystyle{ v }[/math] is a regular vertex with [math]\displaystyle{ s^{-1}(v) \subseteq H }[/math], then [math]\displaystyle{ v \in H }[/math]. The saturated hereditary subsets of [math]\displaystyle{ E }[/math] are partially ordered by inclusion, and they form a lattice with meet [math]\displaystyle{ H_1 \wedge H_2 := H_1 \cap H_2 }[/math] and join [math]\displaystyle{ H_1 \vee H_2 }[/math] defined to be the smallest saturated hereditary subset containing [math]\displaystyle{ H_1 \cup H_2 }[/math].

If [math]\displaystyle{ H }[/math] is a saturated hereditary subset, [math]\displaystyle{ I_H }[/math] is defined to be two-sided ideal in [math]\displaystyle{ L_K(E) }[/math] generated by [math]\displaystyle{ \{ p_v : v \in H \} }[/math]. A two-sided ideal [math]\displaystyle{ I }[/math] of [math]\displaystyle{ L_K(E) }[/math] is called a graded ideal if the [math]\displaystyle{ I }[/math] has a [math]\displaystyle{ \mathbb{Z} }[/math]-grading [math]\displaystyle{ I = \bigoplus_{n \in \mathbb{Z}} I_n }[/math] and [math]\displaystyle{ I_n = L_K(E)_n \cap I }[/math] for all [math]\displaystyle{ n \in \mathbb{Z} }[/math]. The graded ideals are partially ordered by inclusion and form a lattice with meet [math]\displaystyle{ I_1 \wedge I_2 := I_1 \cap I_2 }[/math] and joint [math]\displaystyle{ I_1 \vee I_2 }[/math] defined to be the ideal generated by [math]\displaystyle{ I_1 \cup I_2 }[/math]. For any saturated hereditary subset [math]\displaystyle{ H }[/math], the ideal [math]\displaystyle{ I_H }[/math] is graded.

The following theorem describes how graded ideals of [math]\displaystyle{ L_K(E) }[/math] correspond to saturated hereditary subsets of [math]\displaystyle{ E }[/math].

Theorem: Fix a field [math]\displaystyle{ K }[/math], and let [math]\displaystyle{ E }[/math] be a row-finite graph. Then the following hold:

1. The function [math]\displaystyle{ H \mapsto I_H }[/math] is a lattice isomorphism from the lattice of saturated hereditary subsets of [math]\displaystyle{ E }[/math] onto the lattice of graded ideals of [math]\displaystyle{ L_K(E) }[/math] with inverse given by [math]\displaystyle{ I \mapsto \{ v \in E^0 : p_v \in I \} }[/math].
2. For any saturated hereditary subset [math]\displaystyle{ H }[/math], the quotient [math]\displaystyle{ L_K(E)/I_H }[/math] is [math]\displaystyle{ * }[/math]-isomorphic to [math]\displaystyle{ L_K(E \setminus H) }[/math], where [math]\displaystyle{ E \setminus H }[/math] is the subgraph of [math]\displaystyle{ E }[/math] with vertex set [math]\displaystyle{ (E \setminus H)^0 := E^0 \setminus H }[/math] and edge set [math]\displaystyle{ (E \setminus H)^1 := E^1 \setminus r^{-1}(H) }[/math].
3. For any saturated hereditary subset [math]\displaystyle{ H }[/math], the ideal [math]\displaystyle{ I_H }[/math] is Morita equivalent to [math]\displaystyle{ L_K(E_H) }[/math], where [math]\displaystyle{ E_H }[/math] is the subgraph of [math]\displaystyle{ E }[/math] with vertex set [math]\displaystyle{ E_H^0 := H }[/math] and edge set [math]\displaystyle{ E_H^1 := s^{-1}(H) }[/math].
4. If [math]\displaystyle{ E }[/math] satisfies Condition (K), then every ideal of [math]\displaystyle{ L_K(E) }[/math] is graded, and the ideals of [math]\displaystyle{ L_K(E) }[/math] are in one-to-one correspondence with the saturated hereditary subsets of [math]\displaystyle{ E }[/math].