Lemniscate of Gerono

Short description: Plane algebraic curve

The lemniscate of Gerono

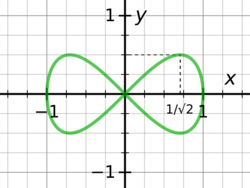
In algebraic geometry, the lemniscate of Gerono, or lemniscate of Huygens, or figure-eight curve, is a plane algebraic curve of degree four and genus zero and is a lemniscate curve shaped like an [math]\displaystyle{ \infty }[/math] symbol, or figure eight. It has equation

[math]\displaystyle{ x^4-x^2+y^2 = 0. }[/math]

It was studied by Camille-Christophe Gerono.

Parameterization

Because the curve is of genus zero, it can be parametrized by rational functions; one means of doing that is

[math]\displaystyle{ x = \frac{t^2-1}{t^2+1},\ y = \frac{2t(t^2-1)}{(t^2+1)^2}. }[/math]

Another representation is

[math]\displaystyle{ x = \cos \varphi,\ y = \sin\varphi\,\cos\varphi = \sin(2\varphi)/2 }[/math]

which reveals that this lemniscate is a special case of a Lissajous figure.

Dual curve

The dual curve (see Plücker formula), pictured below, has therefore a somewhat different character. Its equation is

[math]\displaystyle{ (x^2-y^2)^3 + 8y^4+20x^2y^2-x^4-16y^2=0. }[/math]

Dual to the lemniscate of Gerono

References

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. p. 124. ISBN 0-486-60288-5. https://archive.org/details/catalogofspecial00lawr/page/124. 

External links

• O'Connor, John J.; Robertson, Edmund F., "Figure Eight Curve", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Curves/Eight.html .