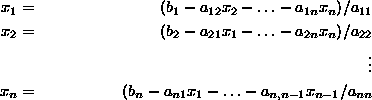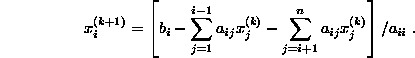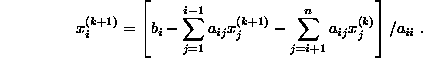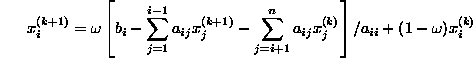Linear equations, iterative solutions
For certain types of systems of linear equations Ax = b methods like Gaussian elimination can become inefficient, e.g. if A is sparse and large. In such cases, iterative methods are preferable. They converge if certain conditions are fulfilled, e.g. if A is diagonally dominant (see Golub89):
In this case, Ax = b can be rewritten in the form
where each line solves separately for the x appearing with the diagonal element of A. Any iterative scheme needs an initial guess x(0), whose quality determines the possibility or the speed of convergence. We obtain the (k+1)st iteration xk+1 if we substitute the kth iteration xk into the right hand side. If we compute all the new values on the left side with all the old values on the right side we obtain the Jacobi iteration :
If we successively use new values of xi as soon as they are computed, we get the Gauss-Seidel iteration :
A variant of this algorithm is the method of Successive Over-Relaxation:
where the over-relaxation parameter ![]() satisfies
satisfies ![]() . For how to determine
. For how to determine ![]() , see Golub89 or Young71.
, see Golub89 or Young71.