Little q-Jacobi polynomials

In mathematics, the little q-Jacobi polynomials p_n(x;a,b;q) are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme, introduced by (Hahn 1949). Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.

Definition

The little q-Jacobi polynomials are given in terms of basic hypergeometric functions by

$p_n(x;a,b;q)={}_2{\varphi }_1(q^{-n},ab{q}^{n+1};aq;q,xq)$

Gallery

The following are a set of animation plots for Little q-Jacobi polynomials, with varying q; three density plots of imaginary, real and modulus in complex space; three set of complex 3D plots of imaginary, real and modulus of the said polynomials.

LITTLE q-JACOBI POLYNOMIALS ABS COMPLEX 3D MAPLE PLOT

LITTLE q-JACOBI POLYNOMIALS IM COMPLEX 3D MAPLE PLOT

LITTLE q-JACOBI POLYNOMIALS RE COMPLEX 3D MAPLE PLOT

LITTLE q-JACOBI POLYNOMIALS ABS DENSITY MAPLE PLOT

LITTLE q-JACOBI POLYNOMIALS IM DENSITY MAPLE PLOT

LITTLE q-JACOBI POLYNOMIALS RE DENSITY MAPLE PLOT

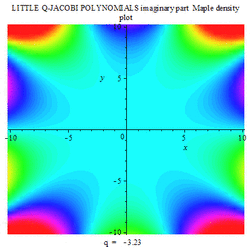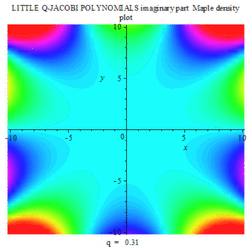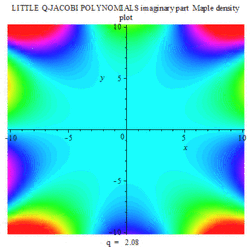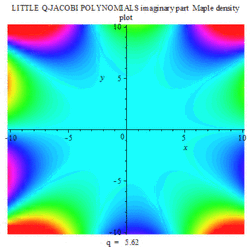References

• Gasper, George; Rahman, Mizan (2004), Basic hypergeometric series, Encyclopedia of Mathematics and its Applications, 96 (2nd ed.), Cambridge University Press, ISBN 978-0-521-83357-8 
• Hahn, Wolfgang (1949), "Über Orthogonalpolynome, die q-Differenzengleichungen genügen", Mathematische Nachrichten 2 (1–2): 4–34, doi:10.1002/mana.19490020103, ISSN 0025-584X 
• Koekoek, Roelof; Lesky, Peter A.; Swarttouw, René F. (2010), Hypergeometric orthogonal polynomials and their q-analogues, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-642-05014-5, ISBN 978-3-642-05013-8 
• Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Little q-Jacobi polynomials", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, http://dlmf.nist.gov/18