Loop dependence analysis

Short description: Process to determine relationships among statements

In computer science, loop dependence analysis is a process which can be used to find dependencies within iterations of a loop with the goal of determining different relationships between statements. These dependent relationships are tied to the order in which different statements access memory locations. Using the analysis of these relationships, execution of the loop can be organized to allow multiple processors to work on different portions of the loop in parallel. This is known as parallel processing. In general, loops can consume a lot of processing time when executed as serial code. Through parallel processing, it is possible to reduce the total execution time of a program through sharing the processing load among multiple processors.

The process of organizing statements to allow multiple processors to work on different portions of a loop is often referred to as parallelization. In order to see how we can exploit parallelization, we have to first analyze the dependencies within individual loops. These dependencies will help determine which statements in the loop need to be completed before other statements can start, and which statements in the loop can be executed in parallel with respect to the other statements in the loop. Two general categories of dependencies that will be analyzed in the loop are data dependencies and control dependencies.

Description

Loop dependence analysis occur on a normalized loop of the form:

for i1 until U1 do
  for i2 until U2 do
    ...
    for in until Un do
      body
    done
    ...
  done
done

where body may contain:

S1  a[f1(i1, ..., in), ..., fm(i1, ..., in)] := ...
    ...
S2  ... := a[h1(i1, ..., in), ..., hm(i1, ..., in)]

Where a is an m-dimensional array and f_n, h_n, etc. are functions mapping from all iteration indexes (i_n) to a memory access in a particular dimension of the array.

For example, in C:

for (i = 0; i < U1; i++)
  for (j = 0; j < U2; j++)
    a[i+4-j] = b[2*i-j] + i*j;

f₁ would be i+4-j, controlling the write on the first dimension of a and h₂ would be 2*i-j, controlling the read on the first dimension of b.

The scope of the problem is to find all possible dependencies between S1 and S2. To be conservative, any dependence which cannot be proven false must be assumed to be true.

Independence is shown by demonstrating that no two instances of S1 and S2 access or modify the same spot in array a. When a possible dependence is found, loop dependence analysis usually makes every attempt to characterize the relationship between dependent instances, as some optimizations may still be possible. It may also be possible to transform the loop to remove or modify the dependence.

In the course of proving or disproving such dependencies, a statement S may be decomposed according to which iteration it comes from. For instance, S[1,3,5] refers to the iteration where i1 = 1, i2 = 3 and i3 = 5. Of course, references to abstract iterations, such as S[d1+1,d2,d3], are both permitted and common.

Data dependence

Further information: Data dependency

Data dependencies show the relationships between the variables in the code. There are three different types of data dependencies:

• True Dependence (sometimes referred to as Flow Dependence)
• Anti Dependence
• Output Dependence

True dependence

A true dependence occurs when a location in memory is written to before it is read. It introduces read-after-write (RAW) hazards because the instruction that reads from the location in memory has to wait until it is written to by the previous instruction or else the reading instruction will read the wrong value. An example of a true dependence is:

S1: a = 5;
S2: b = a;

In this example, there is a true dependence between S1 and S2 because variable a is first written in statement S1 and then variable a is read by statement S2. This true dependence can be represented by S1 →T S2. A true dependence can also be seen when reading and writing between different iterations in a loop. The following example shows a true dependence between different iterations.

for (j = 1; j < n; j++)
    S1: a[j] = a[j-1];

In this example, a true dependence exists between statement S1 in the jth iteration and S1 in the j+1th iteration. There is a true dependence because a value will be written to a[j] in one iteration and then a read occurs by a[j-1] in the next iteration. This true dependence can be represented by S1[j] →T S1[j+1].

Anti dependence

An anti dependence occurs when a location in memory is read before that same location is written to. This introduces write-after-read (WAR) hazards because the instruction that writes the data into a memory location has to wait until that memory location has been read by the previous instruction or else the reading instruction would read the wrong value. An example of an anti dependence is:

S1: a = b;
S2: b = 5;

In this example, there is an anti dependence between statements S1 and S2. This is an anti dependence because variable b is first read in statement S1 and then variable b is written to in statement S2. This can be represented by S1 →A S2. An anti dependence can be seen by different iterations in a loop. The following example shows an example of this case:

for (j = 0; j < n; j++)
    S1: b[j] = b[j+1];

In this example, there is an anti dependence between the jth iteration of S1 and the j+1th element of S1. Here, the j+1th element is read before that same element is written in the next iteration of j. This anti dependence can be represented by S1[j] →A S1[j+1].

Output dependence

An output dependence occurs when a location in memory is written to before that same location is written to again in another statement. This introduces write-after-write (WAW) hazards because the second instruction to write the value to a memory location needs to wait until the first instruction finishes writing data to the same memory location or else when the memory location is read at a later time it will contain the wrong value. An example of an output dependence is:

S1: c = 8; 
S2: c = 15;

In this example, there is an output dependence between statements S1 and S2. Here, the variable c is first written to in S1 and then variable c is written to again in statement S2. This output dependence can be represented by S1 →O S2. An output dependence can be seen by different iterations in a loop. The following code snippet shows an example of this case:

for (j = 0; j < n; j++) {
    S1: c[j] = j;  
    S2: c[j+1] = 5;
}

In this example, there is an output dependence between the jth element in S1 and the j+1th element in S2. Here, c[j+1] in statement S2 is written to in one iteration. In the next iteration, c[j] in statement S2, which is the same memory location as c[j+1] in the previous iteration, is written to again. This output dependence can be represented as S1[j] →O S2[j+1].

Control dependence

Further information: Control dependency

Control dependencies must also be considered when analyzing dependencies between different statements in a loop. Control dependencies are dependencies introduced by the code or the programming algorithm itself. They control the order in which instructions occur within the execution of code. One common example is an "if" statement. "if" statements create branches in a program. The "then" portion of the "if" statement explicitly directs or controls actions to be taken.

// Code block 1 (CORRECT) if (a == b) { c = "controlled"; } d = "uncontrolled";

// Code block 2 (INCORRECT) if (a == b) { } c = "controlled"; d = "uncontrolled";

// Code block 3 (INCORRECT) if (a == b) { c = "controlled"; d = "uncontrolled"; }

In this example, the constraints on control flow are illustrated. Code block 1 shows the correct ordering when using an if statement in the C programming language. Code block 2 illustrates a problem where a statement that is supposed to be controlled by the if statement is no longer controlled by it. Code block 3 illustrates a problem where a statement that is not supposed to be controlled by the "if" statement has now been moved under its control. Both of these two possibilities could lead to improper program execution and must be considered when parallelizing these statements within a loop.

Loop-carried dependence vs. loop independent dependence

Loop-carried dependencies and loop independent dependencies are determined by the relationships between statements in iterations of a loop. When a statement in one iteration of a loop depends in some way on a statement in a different iteration of the same loop, a loop-carried dependence exists. However, if a statement in one iteration of a loop depends only on a statement in the same iteration of the loop, this creates a loop independent dependence.

// Code block 1 for (i = 1; i <= 4; i++) { S1: b[i] = 8; S2: a[i] = b[i-1] + 10; }

// Code block 2 for (i = 0; i < 4; i++) { S1: b[i] = 8; S2: a[i] = b[i] + 10; }

In this example, code block 1 shows loop-dependent dependence between statement S2 iteration i and statement S1 iteration i-1. This is to say that statement S2 cannot proceed until statement S1 in the previous iteration finishes. Code block 2 show loop independent dependence between statements S1 and S2 in the same iteration.

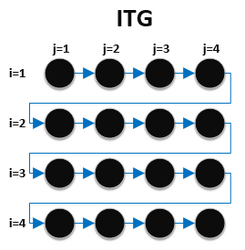
Loop-carried dependence and iteration space traversal graphs

Iteration space traversal graphs (ITG) shows the path that the code takes when traversing through the iterations of the loop. Each iteration is represented with a node. Loop carried dependence graphs (LDG) gives a visual representation of all true dependencies, anti dependencies, and output dependencies that exist between different iterations in a loop. Each iteration is represented with a node.

It is easier to show the difference between the two graphs with a nested for loop.

for (i = 0; i < 4; i++)
    for (j = 0; j < 4; j++)
       S1: a[i][j] = a[i][j-1] * x;

In this example, there is a true dependence between the j iteration of statement S1 and the j+1th statement of S1. This can be represented as S1[i,j] →T S1[i,j+1] The iteration space traversal graph and the loop carried dependence graph is: Iteration Space Traversal Graph: Loop Carried Dependence Graph:

Loop-carried Dependence Graph (LDG)

Iteration-space Traversal Graph (ITG)

See also

• Dependence analysis
• Alias analysis
• DOPIPE
• Loop Level Parallelism
• Loop transformation
• Loop splitting
• Loop fusion
• Loop interchange
• Loop skewing
• Automatic parallelization
• Automatic vectorization