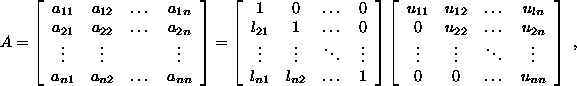Lu decomposition
From HandWiki
Any non-singular matrix A can be expressed as a product A = LU; there exist exactly one lower triangular matrix L and exactly one upper triangular matrix U of the form:
if row exchanges (partial pivoting) are not necessary. With pivoting, we have to introduce a permutation matrix P, P being an identity matrix with interchanged (swapped) rows. Instead of A one then decomposes PA:
The LU decomposition can be performed in a way similar to Gaussian elimination.
LU decomposition is useful, e.g. for the solution of the exactly determined system of linear equations Ax = b, when there is more than one right-hand side b. With A = LU the system becomes
or
c can be computed by forward substitution and x by back substitution. (see Golub89).