Möbius ladder

Short description: Cycle graph with all opposite nodes linked

Möbius ladder
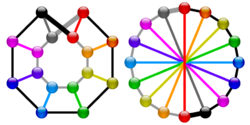Two views of the Möbius ladder M16. For an animation showing the transformation between the two views, see this file.
Vertices	n (even number)
Edges	n + n/2
Girth	4 (for even n > 4)
Chromatic number	3
Chromatic index	3
Genus	1 (for even n > 4)
Properties	Cubic Circulant Vertex-transitive Apex (for even n > 4) Toroidal (for even n > 4) Edge-transitive (for n = 4, 6) Bipartite (for non-doubly even n)
Notation	Mn
Table of graphs and parameters

In graph theory, the Möbius ladder M_n, for even numbers n, is formed from an n-cycle by adding edges (called "rungs") connecting opposite pairs of vertices in the cycle. It is a cubic, circulant graph, so-named because (with the exception of M₆ (the utility graph K_3,3), M_n has exactly n/2 four-cycles which link together by their shared edges to form a topological Möbius strip. Möbius ladders were named and first studied by Guy and Harary (1967).

Properties

For every even n > 4, the Möbius ladder M_n is a nonplanar apex graph, meaning that it cannot be drawn without crossings in the plane but removing one vertex allows the remaining graph to be drawn without crossings. These graphs have crossing number one, and can be embedded without crossings on a torus or projective plane. Thus, they are examples of toroidal graphs. (Li 2005) explores embeddings of these graphs onto higher genus surfaces.

Möbius ladders are vertex-transitive – they have symmetries taking any vertex to any other vertex – but (with the exceptions of M₄ and M₆) they are not edge-transitive. The edges from the cycle from which the ladder is formed can be distinguished from the rungs of the ladder, because each cycle edge belongs to a single 4-cycle, while each rung belongs to two such cycles. Therefore, there is no symmetry taking a cycle edge to a rung edge or vice versa.

When n ≡ 2 (mod 4), M_n is bipartite. When n ≡ 0 (mod 4), it is not bipartite. The endpoints of each rung are an even distance apart in the initial cycle, so adding each rung creates an odd cycle. In this case, because the graph is 3-regular but not bipartite, by Brooks' theorem it has chromatic number 3. (De Mier Noy) show that the Möbius ladders are uniquely determined by their Tutte polynomials.

The Möbius ladder M₈ has 392 spanning trees; it and M₆ have the most spanning trees among all cubic graphs with the same number of vertices. However, the 10-vertex cubic graph with the most spanning trees is the Petersen graph, which is not a Möbius ladder.

The Tutte polynomials of the Möbius ladders may be computed by a simple recurrence relation.

Graph minors

The Wagner graph M₈

Möbius ladders play an important role in the theory of graph minors. The earliest result of this type is a theorem of Klaus Wagner (1937) that graphs with no K₅ minor can be formed by using clique-sum operations to combine planar graphs and the Möbius ladder M₈; for this reason M₈ is called the Wagner graph.

(Gubser 1996) defines an almost-planar graph to be a nonplanar graph for which every nontrivial minor is planar; he shows that 3-connected almost-planar graphs are Möbius ladders or members of a small number of other families, and that other almost-planar graphs can be formed from these by a sequence of simple operations.

(Maharry 2000) shows that almost all graphs that do not have a cube minor can be derived by a sequence of simple operations from Möbius ladders.

Chemistry and physics

(Walba Richards) first synthesized molecular structures in the form of a Möbius ladder, and since then this structure has been of interest in chemistry and chemical stereography, especially in view of the ladder-like form of DNA molecules. With this application in mind, Flapan (1989) studies the mathematical symmetries of embeddings of Möbius ladders in R³. In particular, as she shows, every three-dimensional embedding of a Möbius ladder with an odd number of rungs is topologically chiral: it cannot be converted into its mirror image by a continuous deformation of space without passing one edge through another. On the other hand, Möbius ladders with an even number of rungs all do have embeddings into R³ that can be deformed into their mirror images.

Möbius ladders have also been used as the shape of a superconducting ring in experiments to study the effects of conductor topology on electron interactions.

Combinatorial optimization

Möbius ladders have also been used in computer science, as part of integer programming approaches to problems of set packing and linear ordering. Certain configurations within these problems can be used to define facets of the polytope describing a linear programming relaxation of the problem; these facets are called Möbius ladder constraints.

See also

• Ladder graph
• Prism graph

References

• "Recursive families of graphs". Journal of Combinatorial Theory. Series B 12 (2): 123–131. 1972. doi:10.1016/0095-8956(72)90016-0. 
• Bolotashvili, G.; Kovalev, M.; Girlich, E. (1999). "New facets of the linear ordering polytope". SIAM Journal on Discrete Mathematics 12 (3): 326–336. doi:10.1137/S0895480196300145. 
• Borndörfer, Ralf; Weismantel, Robert (2000). "Set packing relaxations of some integer programs". Mathematical Programming. Series A 88 (3): 425–450. doi:10.1007/PL00011381. 
• Deng, Wen-Ji; Xu, Ji-Huan; Liu, Ping (2002). "Period halving of persistent currents in mesoscopic Möbius ladders". Chinese Physics Letters 19 (7): 988–991. doi:10.1088/0256-307X/19/7/333. Bibcode: 2002ChPhL..19..988D. 
• Mathematische Annalen 283 (2): 271–283. 1989. doi:10.1007/BF01446435. 
• "On the acyclic subgraph polytope". Mathematical Programming 33: 28–42. 1985a. doi:10.1007/BF01582009. 
• Grötschel, M.; Jünger, M.; Reinelt, G. (1985b). "Facets of the linear ordering polytope". Mathematical Programming 33: 43–60. doi:10.1007/BF01582010. 
• Gubser, Bradley S. (1996). "A characterization of almost-planar graphs". Combinatorics, Probability and Computing 5 (3): 227–245. doi:10.1017/S0963548300002005. 
• "On the Möbius ladders". Canadian Mathematical Bulletin 10 (4): 493–496. 1967. doi:10.4153/CMB-1967-046-4. 
• Jakobson, Dmitry (1999). On some extremal problems in graph theory. https://archive.org/details/arxiv-math9907050. 
• Li, De-ming (2005). "Genus distributions of Möbius ladders". Northeastern Mathematics Journal 21 (1): 70–80. 
• Maharry, John (2000). "A characterization of graphs with no cube minor". Journal of Combinatorial Theory. Series B 80 (2): 179–201. doi:10.1006/jctb.2000.1968. http://rave.ohiolink.edu/etdc/view?acc_num=osu1487934589975195. 
• McSorley, John P. (1998). "Counting structures in the Möbius ladder". Discrete Mathematics 184 (1–3): 137–164. doi:10.1016/S0012-365X(97)00086-1. https://opensiuc.lib.siu.edu/math_articles/93. 
• De Mier, Anna; Noy, Marc (2004). "On graphs determined by their Tutte polynomials". Graphs and Combinatorics 20 (1): 105–119. doi:10.1007/s00373-003-0534-z. 
• Mila, Frédéric; Stafford, C. A.; Capponi, Sylvain (1998). "Persistent currents in a Möbius ladder: A test of interchain coherence of interacting electrons". Physical Review B 57 (3): 1457–1460. doi:10.1103/PhysRevB.57.1457. Bibcode: 1998PhRvB..57.1457M. http://www.physics.arizona.edu/~stafford/pdf/moebius.pdf. 
• Newman, Alantha; Vempala, Santosh (2001). "Fences are futile: on relaxations for the linear ordering problem". 2081. Berlin: Springer-Verlag. pp. 333–347. doi:10.1007/3-540-45535-3_26. http://theory.lcs.mit.edu/~alantha/papers/ipco01.ps. Retrieved 2006-10-08. 
• Simon, Jonathan (1992). "Knots and chemistry". 45. Providence, RI: American Mathematical Society. pp. 97–130. 
• Valdes, L. (1991). "Extremal properties of spanning trees in cubic graphs". 85. pp. 143–160. 
• "Über eine Eigenschaft der ebenen Komplexe". Mathematische Annalen 114: 570–590. 1937. doi:10.1007/BF01594196. 
• Walba, D.; Richards, R.; Haltiwanger, R. C. (1982). "Total synthesis of the first molecular Möbius strip". Journal of the American Chemical Society 104 (11): 3219–3221. doi:10.1021/ja00375a051. 

External links

• Weisstein, Eric W.. "Möbius Ladder". http://mathworld.wolfram.com/MoebiusLadder.html.