Macdonald polynomials

In mathematics, Macdonald polynomials P_λ(x; t,q) are a family of orthogonal symmetric polynomials in several variables, introduced by Macdonald in 1987. He later introduced a non-symmetric generalization in 1995. Macdonald originally associated his polynomials with weights λ of finite root systems and used just one variable t, but later realized that it is more natural to associate them with affine root systems rather than finite root systems, in which case the variable t can be replaced by several different variables t=(t₁,...,t_k), one for each of the k orbits of roots in the affine root system. The Macdonald polynomials are polynomials in n variables x=(x₁,...,x_n), where n is the rank of the affine root system. They generalize many other families of orthogonal polynomials, such as Jack polynomials and Hall–Littlewood polynomials and Askey–Wilson polynomials, which in turn include most of the named 1-variable orthogonal polynomials as special cases. Koornwinder polynomials are Macdonald polynomials of certain non-reduced root systems. They have deep relationships with affine Hecke algebras and Hilbert schemes, which were used to prove several conjectures made by Macdonald about them.

Definition

First fix some notation:

• R is a finite root system in a real vector space V.
• R⁺ is a choice of positive roots, to which corresponds a positive Weyl chamber.
• W is the Weyl group of R.
• Q is the root lattice of R (the lattice spanned by the roots).
• P is the weight lattice of R (containing Q).
• An ordering on the weights: [math]\displaystyle{ \mu \le \lambda }[/math] if and only if [math]\displaystyle{ \lambda-\mu }[/math] is a nonnegative linear combination of simple roots.
• P⁺ is the set of dominant weights: the elements of P in the positive Weyl chamber.
• ρ is the Weyl vector: half the sum of the positive roots; this is a special element of P⁺ in the interior of the positive Weyl chamber.
• F is a field of characteristic 0, usually the rational numbers.
• A = F(P) is the group algebra of P, with a basis of elements written e^λ for λ ∈ P.
• If f = e^λ, then f means e^−λ, and this is extended by linearity to the whole group algebra.
• m_μ = Σ_{λ ∈ Wμ}e^λ is an orbit sum; these elements form a basis for the subalgebra A^W of elements fixed by W.
• [math]\displaystyle{ (a;q)_\infty = \prod_{r\ge0}(1-aq^r) }[/math], the infinite q-Pochhammer symbol.
• [math]\displaystyle{ \Delta= \prod_{\alpha\in R} {(e^\alpha; q)_\infty \over (te^\alpha; q)_\infty}. }[/math]
• [math]\displaystyle{ \langle f,g\rangle=(\text{constant term of }f \overline g \Delta)/|W| }[/math] is the inner product of two elements of A, at least when t is a positive integer power of q.

The Macdonald polynomials P_λ for λ ∈ P⁺ are uniquely defined by the following two conditions:

[math]\displaystyle{ P_\lambda=\sum_{\mu\le \lambda}u_{\lambda\mu}m_\mu }[/math] where u_λμ is a rational function of q and t with u_λλ = 1;

P_λ and P_μ are orthogonal if λ < μ.

In other words, the Macdonald polynomials are obtained by orthogonalizing the obvious basis for A^W. The existence of polynomials with these properties is easy to show (for any inner product). A key property of the Macdonald polynomials is that they are orthogonal: 〈P_λ, P_μ〉 = 0 whenever λ ≠ μ. This is not a trivial consequence of the definition because P⁺ is not totally ordered, and so has plenty of elements that are incomparable. Thus one must check that the corresponding polynomials are still orthogonal. The orthogonality can be proved by showing that the Macdonald polynomials are eigenvectors for an algebra of commuting self-adjoint operators with 1-dimensional eigenspaces, and using the fact that eigenspaces for different eigenvalues must be orthogonal.

In the case of non-simply-laced root systems (B, C, F, G), the parameter t can be chosen to vary with the length of the root, giving a three-parameter family of Macdonald polynomials. One can also extend the definition to the nonreduced root system BC, in which case one obtains a six-parameter family (one t for each orbit of roots, plus q) known as Koornwinder polynomials. It is sometimes better to regard Macdonald polynomials as depending on a possibly non-reduced affine root system. In this case, there is one parameter t associated to each orbit of roots in the affine root system, plus one parameter q. The number of orbits of roots can vary from 1 to 5.

Examples

• If q = t the Macdonald polynomials become the Weyl characters of the representations of the compact group of the root system, or the Schur functions in the case of root systems of type A.
• If q = 0 the Macdonald polynomials become the (rescaled) zonal spherical functions for a semisimple p-adic group, or the Hall–Littlewood polynomials when the root system has type A.
• If t=1 the Macdonald polynomials become the sums over W orbits, which are the monomial symmetric functions when the root system has type A.
• If we put t = q^α and let q tend to 1 the Macdonald polynomials become Jack polynomials when the root system is of type A, and Heckman–Opdam polynomials for more general root systems.
• For the affine root system A₁, the Macdonald polynomials are the Rogers polynomials.
• For the non-reduced rank 1 affine root system of type (C∨1, C₁), the Macdonald polynomials are the Askey–Wilson polynomials, which in turn include as special cases most of the named families of orthogonal polynomials in 1 variable.
• For the non-reduced affine root system of type (C∨n, C_n), the Macdonald polynomials are the Koornwinder polynomials.

The Macdonald constant term conjecture

If t = q^k for some positive integer k, then the norm of the Macdonald polynomials is given by

[math]\displaystyle{ \langle P_\lambda, P_\lambda\rangle = \prod_{\alpha\in R, \alpha\gt 0} \prod_{0\lt i\lt k} {1-q^{(\lambda+k\rho,2\alpha/(\alpha,\alpha))+i} \over 1-q^{(\lambda+k\rho,2\alpha/(\alpha,\alpha))-i}}. }[/math]

This was conjectured by Macdonald (1982) as a generalization of the Dyson conjecture, and proved for all (reduced) root systems by Cherednik (1995) using properties of double affine Hecke algebras. The conjecture had previously been proved case-by-case for all roots systems except those of type E_n by several authors.

There are two other conjectures which together with the norm conjecture are collectively referred to as the Macdonald conjectures in this context: in addition to the formula for the norm, Macdonald conjectured a formula for the value of P_λ at the point t^ρ, and a symmetry

[math]\displaystyle{ \frac{P_\lambda(\dots,q^{\mu_i}t^{\rho_i},\dots)}{P_\lambda(t^\rho)} = \frac{P_\mu(\dots,q^{\lambda_i}t^{\rho_i},\dots)}{P_\mu(t^\rho)}. }[/math]

Again, these were proved for general reduced root systems by Cherednik (1995), using double affine Hecke algebras, with the extension to the BC case following shortly thereafter via work of van Diejen, Noumi, and Sahi.

The Macdonald positivity conjecture

In the case of roots systems of type A_n−1 the Macdonald polynomials are simply symmetric polynomials in n variables with coefficients that are rational functions of q and t. A certain transformed version [math]\displaystyle{ \widetilde{H}_\mu }[/math] of the Macdonald polynomials (see Combinatorial formula below) form an orthogonal basis of the space of symmetric functions over [math]\displaystyle{ \mathbb{Q}(q,t) }[/math], and therefore can be expressed in terms of Schur functions [math]\displaystyle{ s_\lambda }[/math]. The coefficients K_λμ(q,t) of these relations are called Kostka–Macdonald coefficients or qt-Kostka coefficients. Macdonald conjectured that the Kostka–Macdonald coefficients were polynomials in q and t with non-negative integer coefficients. These conjectures are now proved; the hardest and final step was proving the positivity, which was done by Mark Haiman (2001), by proving the n! conjecture.

It is still a central open problem in algebraic combinatorics to find a combinatorial formula for the qt-Kostka coefficients.

n! conjecture

The n! conjecture of Adriano Garsia and Mark Haiman states that for each partition μ of n the space

[math]\displaystyle{ D_\mu =C[\partial_x,\partial_y]\,\Delta_\mu }[/math]

spanned by all higher partial derivatives of

[math]\displaystyle{ \Delta_\mu = \det (x_i^{p_j}y_i^{q_j})_{1\le i,j,\le n} }[/math]

has dimension n!, where (p_j, q_j) run through the n elements of the diagram of the partition μ, regarded as a subset of the pairs of non-negative integers. For example, if μ is the partition 3 = 2 + 1 of n = 3 then the pairs (p_j, q_j) are (0, 0), (0, 1), (1, 0), and the space D_μ is spanned by

[math]\displaystyle{ \Delta_\mu=x_1y_2+x_2y_3+x_3y_1-x_2y_1-x_3y_2-x_1y_3 }[/math]

[math]\displaystyle{ y_2-y_3 }[/math]

[math]\displaystyle{ y_3-y_1 }[/math]

[math]\displaystyle{ x_3-x_2 }[/math]

[math]\displaystyle{ x_1-x_3 }[/math]

[math]\displaystyle{ 1 }[/math]

which has dimension 6 = 3!.

Haiman's proof of the Macdonald positivity conjecture and the n! conjecture involved showing that the isospectral Hilbert scheme of n points in a plane was Cohen–Macaulay (and even Gorenstein). Earlier results of Haiman and Garsia had already shown that this implied the n! conjecture, and that the n! conjecture implied that the Kostka–Macdonald coefficients were graded character multiplicities for the modules D_μ. This immediately implies the Macdonald positivity conjecture because character multiplicities have to be non-negative integers.

Ian Grojnowski and Mark Haiman found another proof of the Macdonald positivity conjecture by proving a positivity conjecture for LLT polynomials.

Combinatorial formula for the Macdonald polynomials

In 2005, J. Haglund, M. Haiman and N. Loehr gave the first proof of a combinatorial interpretation of the Macdonald polynomials. In 1988, I.G. Macdonald gave the second proof of a combinatorial interpretation of the Macdonald polynomials (equations (4.11) and (5.13)). Macdonald’s formula is different to that in Haglund, Haiman, and Loehr's work, with many fewer terms (this formula is proved also in Macdonald's seminal work, Ch. VI (7.13)). While very useful for computation and interesting in its own right, their combinatorial formulas do not immediately imply positivity of the Kostka-Macdonald coefficients [math]\displaystyle{ K_{\lambda \mu}(q,t), }[/math] as the give the decomposition of the Macdonald polynomials into monomial symmetric functions rather than into Schur functions.

Written in the transformed Macdonald polynomials [math]\displaystyle{ \widetilde{H}_\mu }[/math] rather than the usual [math]\displaystyle{ P_\lambda }[/math], they are

[math]\displaystyle{ \widetilde{H}_\mu(x;q,t) = \sum_{\sigma:\mu \to \Z_+} q^{inv(\sigma)}t^{maj(\sigma)} x^{\sigma} }[/math]

where σ is a filling of the Young diagram of shape μ, inv and maj are certain combinatorial statistics (functions) defined on the filling σ. This formula expresses the Macdonald polynomials in infinitely many variables. To obtain the polynomials in n variables, simply restrict the formula to fillings that only use the integers 1, 2, ..., n. The term x^σ should be interpreted as [math]\displaystyle{ x_1^{\sigma_1} x_2^{\sigma_2} \cdots }[/math] where σ_i is the number of boxes in the filling of μ with content i.

This depicts the arm and the leg of a square of a Young diagram. The arm is the number of squares to its right, and the leg is the number of squares above it.

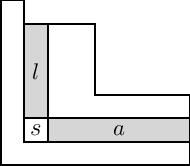
The transformed Macdonald polynomials [math]\displaystyle{ \widetilde{H}_\mu(x;q,t) }[/math] in the formula above are related to the classical Macdonald polynomials [math]\displaystyle{ P_{\lambda} }[/math] via a sequence of transformations. First, the integral form of the Macdonald polynomials, denoted [math]\displaystyle{ J_\lambda(x;q,t) }[/math], is a re-scaling of [math]\displaystyle{ P_\lambda(x;q,t) }[/math] that clears the denominators of the coefficients:

[math]\displaystyle{ J_\lambda(x;q,t)=\prod_{s\in D(\lambda)}(1-q^{a(s)}t^{1+l(s)})\cdot P_\lambda(x;q,t) }[/math]

where [math]\displaystyle{ D(\lambda) }[/math] is the collection of squares in the Young diagram of [math]\displaystyle{ \lambda }[/math], and [math]\displaystyle{ a(s) }[/math] and [math]\displaystyle{ l(s) }[/math] denote the arm and leg of the square [math]\displaystyle{ s }[/math], as shown in the figure. Note: The figure at right uses French notation for tableau, which is flipped vertically from the English notation used on the Wikipedia page for Young diagrams. French notation is more commonly used in the study of Macdonald polynomials.

The transformed Macdonald polynomials [math]\displaystyle{ \widetilde{H}_\mu(x;q,t) }[/math] can then be defined in terms of the [math]\displaystyle{ J_\mu }[/math]'s. We have

[math]\displaystyle{ \widetilde{H}_\mu(x;q,t)=t^{-n(\mu)}J_\mu\left[\frac{X}{1-t^{-1}};q,t^{-1}\right] }[/math]

where

[math]\displaystyle{ n(\mu)=\sum_{i}\mu_i\cdot (i-1). }[/math]

The bracket notation above denotes plethystic substitution.

This formula can be used to prove Knop and Sahi's formula for the Jack polynomials.

Non-symmetric Macdonald polynomials

In 1995, Macdonald introduced a non-symmetric analogue of the symmetric Macdonald polynomials, and the symmetric Macdonald polynomials can easily be recovered from the non-symmetric counterpart. In his original definition, he shows that the non-symmetric Macdonald polynomials are a unique family of polynomials orthogonal to a certain inner product, as well as satisfying a triangularity property when expanded in the monomial basis.

In 2007, Haglund, Haiman and Loehr gave a combinatorial formula for the non-symmetric Macdonald polynomials.

The non-symmetric Macdonald polynomials specialize to Demazure characters by taking q=t=0, and to key polynomials when q=t=∞.

Combinatorial formulae based on the exclusion process

In 2018, S. Corteel, O. Mandelshtam, and L. Williams used the exclusion process to give a direct combinatorial characterization of both symmetric and nonsymmetric Macdonald polynomials. Their results differ from the earlier work of Haglund in part because they give a formula directly for the Macdonald polynomials rather than a transformation thereof. They develop the concept of a multiline queue, which is a matrix containing balls or empty cells together with a mapping between balls and their neighbors and a combinatorial labeling mechanism. The nonsymmetric Macdonald polynomial then satisfies:

[math]\displaystyle{ E_{\lambda}(\textbf{x};q,t)=\sum_Q \mathrm{wt}(Q) }[/math]

where the sum is over all [math]\displaystyle{ L\times n }[/math] multiline queues of type [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \mathrm{wt} }[/math] is a weighting function mapping those queues to specific polynomials. The symmetric Macdonald polynomial satisfies:

[math]\displaystyle{ P_{\lambda}(\textbf{x};q,t)=\sum_{\mu}E_{\mu}(x_1,...,x_n;q,t)=\sum_{\mu}\sum_Q \mathrm{wt}(Q) }[/math]

where the outer sum is over all distinct compositions [math]\displaystyle{ \mu }[/math] which are permutations of [math]\displaystyle{ \lambda }[/math], and the inner sum is as before.

Bibliography

• Cherednik, Ivan (1995), "Double Affine Hecke Algebras and Macdonald's Conjectures", Annals of Mathematics, Second Series (Annals of Mathematics) 141 (1): 191–216, doi:10.2307/2118632, ISSN 0003-486X 
• Garsia, Adriano; Remmel, Jeffrey B. (March 15, 2005), "Breakthroughs in the theory of Macdonald polynomials", PNAS 102 (11): 3891–3894, doi:10.1073/pnas.0409705102, PMID 15753285, Bibcode: 2005PNAS..102.3891G 
• Mark Haiman Combinatorics, symmetric functions, and Hilbert schemes Current Developments in Mathematics 2002, no. 1 (2002), 39–111.
• Haiman, Mark Notes on Macdonald polynomials and the geometry of Hilbert schemes. Symmetric functions 2001: surveys of developments and perspectives, 1–64, NATO Sci. Ser. II Math. Phys. Chem., 74, Kluwer Acad. Publ., Dordrecht, 2002.MR2059359
• Haiman, Mark (2001), "Hilbert schemes, polygraphs, and the Macdonald positivity conjecture", J. Amer. Math. Soc. 14 (4): 941–1006, doi:10.1090/S0894-0347-01-00373-3 
• Kirillov, A. A. (1997), "Lectures on affine Hecke algebras and Macdonald's conjectures", Bull. Amer. Math. Soc. 34 (3): 251–292, doi:10.1090/S0273-0979-97-00727-1, https://www.ams.org/bull/1997-34-03/S0273-0979-97-00727-1/home.html 
• Macdonald, I. G. (1982), "Some conjectures for root systems", SIAM Journal on Mathematical Analysis 13 (6): 988–1007, doi:10.1137/0513070, ISSN 0036-1410 
• Macdonald, I. G. Symmetric functions and Hall polynomials. Second edition. Oxford Mathematical Monographs. Oxford Science Publications. The Clarendon Press, Oxford University Press, New York, 1995. x+475 pp. ISBN 0-19-853489-2 MR1354144
• Macdonald, I. G. Symmetric functions and orthogonal polynomials. Dean Jacqueline B. Lewis Memorial Lectures presented at Rutgers University, New Brunswick, NJ. University Lecture Series, 12. American Mathematical Society, Providence, RI, 1998. xvi+53 pp. ISBN 0-8218-0770-6 MR1488699
• Macdonald, I. G. Affine Hecke algebras and orthogonal polynomials. Séminaire Bourbaki 797 (1995).
• Macdonald, I. G. (2000–2001), "Orthogonal polynomials associated with root systems", Séminaire Lotharingien de Combinatoire 45: Art. B45a 
• Macdonald, I. G. (2003), Affine Hecke algebras and orthogonal polynomials, Cambridge Tracts in Mathematics, 157, Cambridge: Cambridge University Press, pp. x+175, ISBN 978-0-521-82472-9 

External links

• Mike Zabrocki's page about Macdonald polynomials.
• Some of Haiman's papers about Macdonald polynomials.