Magnetic dip
Magnetic dip, dip angle, or magnetic inclination is the angle made with the horizontal by Earth's magnetic field lines. This angle varies at different points on Earth's surface. Positive values of inclination indicate that the magnetic field of Earth is pointing downward, into Earth, at the point of measurement, and negative values indicate that it is pointing upward. The dip angle is in principle the angle made by the needle of a vertically held compass, though in practice ordinary compass needles may be weighted against dip or may be unable to move freely in the correct plane. The value can be measured more reliably with a special instrument typically known as a dip circle.
Dip angle was discovered by the German engineer Georg Hartmann in 1544.[1] A method of measuring it with a dip circle was described by Robert Norman in England in 1581.[2]
Explanation
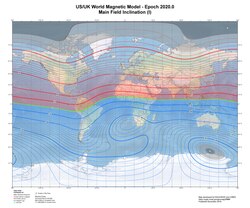
Magnetic dip results from the tendency of a magnet to align itself with lines of magnetic field. As Earth's magnetic field lines are not parallel to the surface, the north end of a compass needle will point upward in the southern hemisphere (negative dip) or downward in the northern hemisphere (positive dip) . The range of dip is from -90 degrees (at the South Magnetic Pole) to +90 degrees (at the North Magnetic Pole).[3] Contour lines along which the dip measured at Earth's surface is equal are referred to as isoclinic lines. The locus of the points having zero dip is called the magnetic equator or aclinic line.[4]
Calculation for a given latitude
The inclination [math]\displaystyle{ I }[/math] is defined locally for the magnetic field due to Earth's core, and has a positive value if the field points below the horizontal (i.e. into Earth). Here we show how to determine the value of [math]\displaystyle{ I }[/math] at a given latitude, following the treatment given by Fowler.[5]
Outside Earth's core we consider Maxwell's equations in a vacuum, [math]\displaystyle{ \nabla \times \textbf{H}_c = \textbf{0} }[/math] and [math]\displaystyle{ \nabla \cdot \textbf{B}_c = 0 }[/math] where [math]\displaystyle{ \textbf{B}_c = \mu_0\textbf{H}_c }[/math] and the subscript [math]\displaystyle{ c }[/math] denotes the core as the origin of these fields. The first means we can introduce the scalar potential [math]\displaystyle{ \phi_c }[/math] such that [math]\displaystyle{ \textbf{H}_c = -\nabla \phi_c }[/math], while the second means the potential satisfies the Laplace equation [math]\displaystyle{ \nabla^2 \phi_c = 0 }[/math].
Solving to leading order gives the magnetic dipole potential
[math]\displaystyle{ \phi_c = \frac{\textbf{m}\cdot \textbf{r}}{4 \pi r^3} }[/math]
and hence the field
[math]\displaystyle{ \textbf{B}_c = -\mu_o \nabla \phi_c = \frac{\mu_o}{4\pi}\big[ \frac{ 3\hat{\textbf{r}}(\hat{\textbf{r}}\cdot \textbf{m})-\textbf{m}} {r^3} \big] }[/math]
for magnetic moment [math]\displaystyle{ \textbf{m} }[/math] and position vector [math]\displaystyle{ \textbf{r} }[/math] on Earth's surface. From here it can be shown that the inclination [math]\displaystyle{ I }[/math] as defined above satisfies (from [math]\displaystyle{ \tan I = B_r / B_{\theta} }[/math])
[math]\displaystyle{ \tan I = 2\tan \lambda }[/math]
where [math]\displaystyle{ \lambda }[/math] is the latitude of the point on Earth's surface.
Practical importance
The phenomenon is especially important in aviation. Magnetic compasses on airplanes are made so that the center of gravity is significantly lower than the pivot point. As a result, the vertical component of the magnetic force is too weak to tilt the compass card significantly out of the horizontal plane, thus minimizing the dip angle shown in the compass. However, this also causes the airplane's compass to give erroneous readings during banked turns (turning error) and airspeed changes (acceleration error).[6]
Turning error
Magnetic dip shifts the center of gravity of the compass card, causing temporary inaccurate readings when turning North or South. As the aircraft turns, the force that results from the magnetic dip causes the float assembly to swing in the same direction that the float turns. This compass error is amplified with the proximity to either magnetic pole.[6]
To compensate for turning errors, pilots in the northern hemisphere will have to "undershoot" the turn when turning North, stopping the turn prior to the compass rotating to the correct heading; and "overshoot" the turn when turning South by stopping later than the compass. The effect is the opposite in the southern hemisphere.[6]
Acceleration error
.gif)
The acceleration errors occur because the compass card tilts on its mount when under acceleration.[7] In the Northern Hemisphere, when accelerating on either an easterly or westerly heading, the error appears as a turn indication toward the north. When decelerating on either of these headings, the compass indicates a turn toward the south.[6] The effect is the opposite in the Southern Hemisphere.
Balancing
Compass needles are often weighted during manufacture to compensate for magnetic dip, so that they will balance roughly horizontally. This balancing is latitude-dependent; see Compass balancing (magnetic dip).
See also
- Aircraft compass turns
- Magnetic declination
- South Atlantic Anomaly
References
- ↑ Murray, Charles (2003). Human Accomplishment (First ed.). HarperCollins. p. 176. ISBN 9780060192471. https://archive.org/details/humanaccomplishm00murr.
- ↑ Norman, Robert (1581). The newe attractive: shewing the nature, propertie, and manifold vertues of the loadstone: with the declination of the needle, touched therewith under the plaine of the horizon. https://archive.org/details/neweattractives00normgoog.
- ↑ Mussett, Alan E.; Khan, M. Aftab (2000). Looking into the earth : an introduction to geological geophysics. Cambridge: Cambridge University Press. pp. 140. ISBN 0521780853. OCLC 43227335. https://archive.org/details/lookingintoearth00muss.
- ↑ Wood, James, ed (1907). "Aclinic Line". The Nuttall Encyclopædia. http://www.fromoldbooks.org/Wood-NuttallEncyclopaedia/a/aclinicline.html.
- ↑ Fowler, C. M. R. (2004-12-20) (in en). The Solid Earth: An Introduction to Global Geophysics. Higher Education from Cambridge University Press. p. 49. doi:10.1017/cbo9780511819643. ISBN 9780521893077. https://www.cambridge.org/highereducation/books/the-solid-earth/0A66AC49BB6105F54AACF52D3C3121A4. Retrieved 2022-01-13.
- ↑ 6.0 6.1 6.2 6.3 Template:Cite PHAK
- ↑ Instrument Flying Handbook: FAA-H-8083-15B. Federal Aviation Administration, US Department of Transportation. 2014. pp. 5–13,5–14.
External links
 |  |
