Markov renewal process

From HandWiki
Short description: Generalization of Markov jump processes

Markov renewal processes are a class of random processes in probability and statistics that generalize the class of Markov jump processes. Other classes of random processes, such as Markov chains and Poisson processes, can be derived as special cases among the class of Markov renewal processes, while Markov renewal processes are special cases among the more general class of renewal processes.

Definition

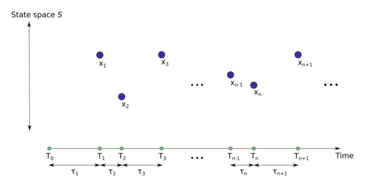
An illustration of a Markov renewal process

In the context of a jump process that takes states in a state space [math]\displaystyle{ \mathrm{S} }[/math], consider the set of random variables [math]\displaystyle{ (X_n,T_n) }[/math], where [math]\displaystyle{ T_n }[/math] represents the jump times and [math]\displaystyle{ X_n }[/math] represents the associated states in the sequence of states (see Figure). Let the sequence of inter-arrival times [math]\displaystyle{ \tau_n=T_n-T_{n-1} }[/math]. In order for the sequence [math]\displaystyle{ (X_n,T_n) }[/math] to be considered a Markov renewal process the following condition should hold:

[math]\displaystyle{ \begin{align} & \Pr(\tau_{n+1}\le t, X_{n+1}=j\mid(X_0, T_0), (X_1, T_1),\ldots, (X_n=i, T_n)) \\[5pt] = {} & \Pr(\tau_{n+1}\le t, X_{n+1}=j\mid X_n=i)\, \forall n \ge1,t\ge0, i,j \in \mathrm{S} \end{align} }[/math]

Relation to other stochastic processes

  1. Let [math]\displaystyle{ X_n }[/math] and [math]\displaystyle{ T_n }[/math] be as defined in the previous statement. Defining a new stochastic process [math]\displaystyle{ Y_t:=X_n }[/math] for [math]\displaystyle{ t \in [T_n,T_{n+1}) }[/math], then the process [math]\displaystyle{ Y_t }[/math] is called a semi-Markov process as it happens in a continuous-time Markov chain. The process is Markovian only at the specified jump instants, justifying the name semi-Markov.[1][2][3] (See also: hidden semi-Markov model.)
  2. A semi-Markov process (defined in the above bullet point) in which all the holding times are exponentially distributed is called a continuous-time Markov chain. In other words, if the inter-arrival times are exponentially distributed and if the waiting time in a state and the next state reached are independent, we have a continuous-time Markov chain.
    [math]\displaystyle{ \begin{align} & \Pr(\tau_{n+1}\le t, X_{n+1}=j\mid(X_0, T_0), (X_1, T_1),\ldots, (X_n=i, T_n)) \\[3pt] = {} & \Pr(\tau_{n+1}\le t, X_{n+1}=j\mid X_n=i) \\[3pt] = {} & \Pr(X_{n+1}=j\mid X_n=i)(1-e^{-\lambda_i t}), \text{ for all } n \ge1,t\ge0, i,j \in \mathrm{S}, i \ne j \end{align} }[/math]
  3. The sequence [math]\displaystyle{ X_n }[/math] in the Markov renewal process is a discrete-time Markov chain. In other words, if the time variables are ignored in the Markov renewal process equation, we end up with a discrete-time Markov chain.
    [math]\displaystyle{ \Pr(X_{n+1}=j\mid X_0, X_1, \ldots, X_n=i)=\Pr(X_{n+1}=j\mid X_n=i)\, \forall n \ge1, i,j \in \mathrm{S} }[/math]
  4. If the sequence of [math]\displaystyle{ \tau }[/math]s is independent and identically distributed, and if their distribution does not depend on the state [math]\displaystyle{ X_n }[/math], then the process is a renewal. So, if the states are ignored and we have a chain of iid times, then we have a renewal process.
    [math]\displaystyle{ \Pr(\tau_{n+1}\le t\mid T_0, T_1, \ldots, T_n)=\Pr(\tau_{n+1}\le t)\, \forall n \ge1, \forall t\ge0 }[/math]

See also


References

  1. ↑ Medhi, J. (1982). Stochastic processes. New York: Wiley & Sons. ISBN 978-0-470-27000-4. 
  2. ↑ Ross, Sheldon M. (1999). Stochastic processes. (2nd ed.). New York [u.a.]: Routledge.. ISBN 978-0-471-12062-9. 
  3. ↑ Barbu, Vlad Stefan; Limnios, Nikolaos (2008). Semi-Markov chains and hidden semi-Markov models toward applications: their use in reliability and DNA analysis. New York: Springer. ISBN 978-0-387-73171-1. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Markov_renewal_process&oldid=3359649"