Erdős–Gyárfás conjecture
| Unsolved problem in mathematics: Must every cubic graph contain a simple cycle of length a power of two? (more unsolved problems in mathematics)
|
| Markström's graph | |
|---|---|
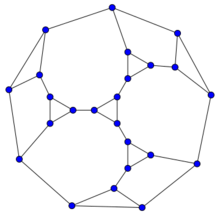 Markström's 24-vertex cubic planar graph with no 4- or 8-cycles, found in a computer search for counterexamples to the Erdős–Gyárfás conjecture. It has, however, cycles with 16 vertices. | |
| Vertices | 24 |
| Edges | 36 |
| Radius | 5 |
| Diameter | 6 |
| Girth | 3 |
| Automorphisms | 3 |
| Table of graphs and parameters | |
In graph theory, the unproven Erdős–Gyárfás conjecture, made in 1995 by the prolific mathematician Paul Erdős and his collaborator András Gyárfás, states that every graph with minimum degree 3 contains a simple cycle whose length is a power of two. Erdős offered a prize of $100 for proving the conjecture, or $50 for a counterexample; it is one of many conjectures of Erdős.
If the conjecture is false, a counterexample would take the form of a graph with minimum degree three having no power-of-two cycles. It is known through computer searches of Gordon Royle and Klas Markström that any counterexample must have at least 17 vertices, and any cubic counterexample must have at least 30 vertices. Markström's searches found four graphs on 24 vertices in which the only power-of-two cycles have 16 vertices. One of these four graphs is planar; however, the Erdős–Gyárfás conjecture is now known to be true for the special case of 3-connected cubic planar graphs ( Heckman Krakovski)
Weaker results relating the degree of a graph to unavoidable sets of cycle lengths are known: there is a set S of lengths, with |S| = O(n0.99), such that every graph with average degree ten or more contains a cycle with its length in S (Verstraëte 2005), and every graph whose average degree is exponential in the iterated logarithm of n necessarily contains a cycle whose length is a power of two (Sudakov Verstraëte). The conjecture is also known to be true for planar claw-free graphs (Daniel Shauger) and for graphs that avoid large induced stars and satisfy additional constraints on their degrees (Shauger 1998).
References
- Daniel, Dale; Shauger, Stephen E. (2001), "A result on the Erdős–Gyárfás conjecture in planar graphs", Proc. 32nd Southeastern Int. Conf. Combinatorics, Graph Theory, and Computing, pp. 129–139.
- Heckman, Christopher Carl; Krakovski, Roi (2013), "Erdös-Gyárfás conjecture for cubic planar graphs", Electronic Journal of Combinatorics 20 (2): P7, doi:10.37236/3252, http://www.combinatorics.org/ojs/index.php/eljc/article/view/v20i2p7.
- Markström, Klas (2004), "Extremal graphs for some problems on cycles in graphs", Congr. Numerantium 171: 179–192, http://abel.math.umu.se/~klasm/Uppsatser/cycex.pdf.
- Shauger, Stephen E. (1998), "Results on the Erdős–Gyárfás conjecture in K1,m-free graphs", Proc. 29th Southeastern Int. Conf. Combinatorics, Graph Theory, and Computing, pp. 61–65
- Sudakov, Benny; Verstraëte, Jacques (2008), "Cycle lengths in sparse graphs", Combinatorica 28 (3): 357–372, doi:10.1007/s00493-008-2300-6.
- Verstraëte, Jacques (2005), "Unavoidable cycle lengths in graphs", Journal of Graph Theory 49 (2): 151–167, doi:10.1002/jgt.20072.
External links
- Exoo, Geoffrey, Graphs Without Cycles of Specified Lengths
- West, Douglas B., Erdős Gyárfás Conjecture on 2-power Cycle Lengths, Open Problems - Graph Theory and Combinatorics
 |

