Star (graph theory)
| Star | |
|---|---|
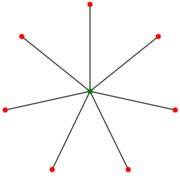 The star S7. (Some authors index this as S8.) | |
| Vertices | k + 1 |
| Edges | k |
| Diameter | 2 |
| Girth | ∞ |
| Chromatic number | 2 |
| Chromatic index | k |
| Properties | Edge-transitive Tree Unit distance Bipartite |
| Notation | Sk |
| Table of graphs and parameters | |
In graph theory, a star Sk is the complete bipartite graph K1,k : a tree with one internal node and k leaves (but no internal nodes and k + 1 leaves when k ≤ 1). Alternatively, some authors define Sk to be the tree of order k with maximum diameter 2; in which case a star of k > 2 has k − 1 leaves.
A star with 3 edges is called a claw.
The star Sk is edge-graceful when k is even and not when k is odd. It is an edge-transitive matchstick graph, and has diameter 2 (when l > 1), girth ∞ (it has no cycles), chromatic index k, and chromatic number 2 (when k > 0). Additionally, the star has large automorphism group, namely, the symmetric group on k letters.
Stars may also be described as the only connected graphs in which at most one vertex has degree greater than one.
Relation to other graph families
Claws are notable in the definition of claw-free graphs, graphs that do not have any claw as an induced subgraph.[1][2] They are also one of the exceptional cases of the Whitney graph isomorphism theorem: in general, graphs with isomorphic line graphs are themselves isomorphic, with the exception of the claw and the triangle K3.[3]
A star is a special kind of tree. As with any tree, stars may be encoded by a Prüfer sequence; the Prüfer sequence for a star K1,k consists of k − 1 copies of the center vertex.[4]
Several graph invariants are defined in terms of stars. Star arboricity is the minimum number of forests that a graph can be partitioned into such that each tree in each forest is a star,[5] and the star chromatic number of a graph is the minimum number of colors needed to color its vertices in such a way that every two color classes together form a subgraph in which all connected components are stars.[6] The graphs of branchwidth 1 are exactly the graphs in which each connected component is a star.[7]
Other applications
The set of distances between the vertices of a claw provides an example of a finite metric space that cannot be embedded isometrically into a Euclidean space of any dimension.[8]
The star network, a computer network modeled after the star graph, is important in distributed computing.
A geometric realization of the star graph, formed by identifying the edges with intervals of some fixed length, is used as a local model of curves in tropical geometry. A tropical curve is defined to be a metric space that is locally isomorphic to a star-shaped metric graph.
See also
- Star (simplicial complex) - a generalization of the concept of a star from a graph to an arbitrary simplicial complex.
References
- ↑ "Claw-free graphs — A survey", Discrete Mathematics 164 (1–3): 87–147, 1997, doi:10.1016/S0012-365X(96)00045-3.
- ↑ "The structure of claw-free graphs", Surveys in combinatorics 2005, London Math. Soc. Lecture Note Ser., 327, Cambridge: Cambridge Univ. Press, 2005, pp. 153–171, http://www.columbia.edu/~mc2775/claws_survey.pdf.
- ↑ "Congruent Graphs and the Connectivity of Graphs", American Journal of Mathematics 54 (1): 150–168, January 1932, doi:10.2307/2371086.
- ↑ Gottlieb, J.; Julstrom, B. A.; Rothlauf, F.; Raidl, G. R. (2001). "Prüfer numbers: A poor representation of spanning trees for evolutionary search". GECCO-2001: Proceedings of the Genetic and Evolutionary Computation Conference. Morgan Kaufmann. pp. 343–350. ISBN 1558607749. https://web.archive.org/web/20060926171652/http://www.ads.tuwien.ac.at/publications/bib/pdf/gottlieb-01.pdf.
- ↑ Hakimi, S. L.; Mitchem, J.; Schmeichel, E. E. (1996), "Star arboricity of graphs", Discrete Math. 149: 93–98, doi:10.1016/0012-365X(94)00313-8
- ↑ Fertin, Guillaume; Raspaud, André (2004), "Star coloring of graphs", Journal of Graph Theory 47 (3): 163–182, doi:10.1002/jgt.20029, https://hal.archives-ouvertes.fr/hal-00307788.
- ↑ "Graph minors. X. Obstructions to tree-decomposition", Journal of Combinatorial Theory 52 (2): 153–190, 1991, doi:10.1016/0095-8956(91)90061-N.
- ↑ "Finite metric spaces–combinatorics, geometry and algorithms", Proc. International Congress of Mathematicians, Beijing, 3, 2002, pp. 573–586, Bibcode: 2003math......4466L
 |
