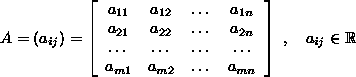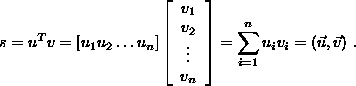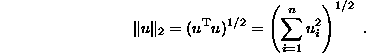Matrix operations

An (m,n) matrix is a rectangular array of real numbers with m rows and n columns

where is the set of real numbers. Most laws of ordinary algebra can be extended to these mathematical objects in a natural way. The sizes of the operands have to agree, of course, depending on the operation.

Addition C = A + B is defined elementwise like C_ij = A_ij + B_ij, multiplication with a scalar B = cA by b_ij = c a_ij, matrix-matrix multiplication C = AB by

In general,  ; matrices are said to commute if AB = BA.

Multiplication is associative: (AB)C = A(BC), left distributive: C(A+B) = CA + CB, and right distributive: (A+B)C = AC + BC.

The transpose matrix is the matrix (a_ji), and . A matrix is symmetric if .

A vector (or column vector) is an (n,1) matrix (a matrix with only 1 column). The row vector, an (1,n) matrix, is obtained by transposition: .

The inner (dot, scalar) product s of 2 vectors u and v is a scalar, and defined as:

The outer product O of 2 vectors u and v is a matrix, and defined as o_ij = u_i v_j:

A set of r vectors is called linearly independent if and only if the only solution to is .

Matrix notation is particularly useful for the description of linear equations.

A matrix A is positive definite if and only if it is symmetric and the quadratic form is positive for all non-zero vectors x.

A square matrix has an inverse if and only if a matrix A^-1 exists with AA^-1 = A^-1A = I with I the identity matrix. (AB)^-1 = B^-1A^-1. In general the inverse A^-1 need not exist for , unlike in ordinary algebra, where a^-1 always exists if . Usually an inverse is not computed explicitly, even if the notation suggests so: if one finds an inverse in a formula like x = A^-1 b, one should think in terms of computing the solution of linear equations.

The pseudoinverse (A⁺) is a generalization of the inverse and exists for any (m,n) matrix.

A matrix Q is orthogonal if , i.e. .

One can use the norm of a vector u ( , defined as the Euclidean length:

The span of a set of vectors is the set of all their linear combinations.

The range of A or column space is the span of the column vectors of A. The span of the row vectors is called the row space (= range of ).

The set of vectors x with Ax = 0 is called the null-space.

The rank of A [rank(A)] is the dimension of the column (or row) space.

The nullity of A [nullity(A)] is the dimension of the null-space.

For more details, see Golub89.