Maxwell's theorem (geometry)

Short description: Given a triangle and a point, constructs a second triangle with a special point

Line segments with identical markings are parallel.
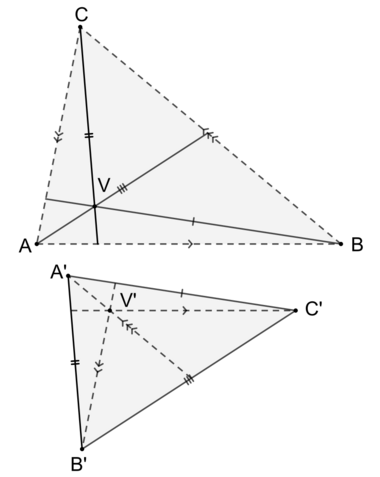
If the sides of the triangle$A^{\prime }{B}^{\prime }{C}^{\prime }$ are parallel to the according cevians of triangle $ABC$, which are intersecting in a common point $V^{\prime }$, then the cevians of triangle $A^{\prime }{B}^{\prime }{C}^{\prime }$, which are parallel to the according sides of triangle $ABC$ intersect in a common point $V^{\prime }$ as well

Maxwell's theorem is the following statement about triangles in the plane.

For a given triangle $ABC$ and a point $V$ not on the sides of that triangle construct a second triangle $A^{\prime }{B}^{\prime }{C}^{\prime }$, such that the side $A^{\prime }{B}^{\prime }$ is parallel to the line segment $CV$, the side $A^{\prime }{C}^{\prime }$ is parallel to the line segment $BV$ and the side $B^{\prime }{C}^{\prime }$ is parallel to the line segment $AV$. Then the parallel to $AB$ through $C^{\prime }$, the parallel to $BC$ through $A^{\prime }$ and the parallel to $AC$ through $B^{\prime }$ intersect in a common point $V^{\prime }$.

The theorem is named after the physicist James Clerk Maxwell (1831–1879), who proved it in his work on reciprocal figures, which are of importance in statics.

References

• Daniel Pedoe: Geometry: A Comprehensive Course. Dover, 1970, pp. 35–36, 114–115
• Daniel Pedoe: "On (what should be) a Well-Known Theorem in Geometry." The American Mathematical Monthly, Vol. 74, No. 7 (August – September, 1967), pp. 839–841 (JSTOR)
• Dao Thanh Oai, Cao Mai Doai, Quang Trung, Kien Xuong, Thai Binh: "Generalizations of some famous classical Euclidean geometry theorems." International Journal of Computer Discovered Mathematics, Vol. 1, No. 3, pp. 13–20

External links

• Maxwell's Theorem at cut-the-knot.org