Medicine:Variable volume pharmacokinetic models

A variable volume pharmacokinetic model can be a drug centered model that assigns a volume of drug distribution to be where the drug is at that time. Another possibility occurs when the body volume is changing in time, which would occur, for example, during dialysis when the volume in which a drug can be distributed is itself changing in time.

History

Perhaps the first drug centered variable volume model was created by Niazi in 1976 Niazi's equations were valid only for sums of exponential terms, that is, models that can also be considered to be compartmental models, and Niazi used the terms variable volume model and mammalian (Sic compartmental) model interchangeably. However, Wesolowski et al. later pointed out that a drug centered variable volume model is actually a single drug volume that increases in time, and as such can have any fit function of the washout type (monotonically non-increasing).

Model

A drug centered variable volume model has the basic equation

             [math]\displaystyle{ C(t)=M(t)/Vd(t) }[/math]   ,             [math]\displaystyle{ (1) }[/math]

where [math]\displaystyle{ C(t) }[/math] is the concentration (see pharmacokinetic metrics), or is concentration related, in the target region being modeled as a function of time, frequently blood plasma or whole blood, [math]\displaystyle{ M(t) }[/math] is the drug mass remaining in the body at that time, and [math]\displaystyle{ Vd(t) }[/math] is the apparent volume of distribution of that drug were it to occupy that volume at the same concentration as in the target region. Since this volume containing drug varies in time, it differs from the static volume of distribution from compartmental models. There is a simple constant factor multiplier between [math]\displaystyle{ Vd(t) }[/math] and the drug's physical volume at that time (an implicit modelling assumption). With reference to Eq. (1), at time zero the mass is the total dose (if rapidly administered, for example in an bolus intravenous injection). Since the dose is a set physical mass, the only method of administering it to mimic the initial volume of drug at that time is to have a small, or even vanishingly small volume of distribution. That makes the concentration very high, or even unbounded large. Now, virtually any washout function can be substituted for a model of concentration. However, if we do not make the initial volume of distribution vanishingly small, then we assume an instant mixing drug delivery in whatever volume the drug is delivered into. That is a common result of using compartmental models, where the assumption of initial drug volumes are often only slightly smaller than that they would be after infinite elapsed time. Such models are not as realistic as using washout functions fit to concentration that can have vanishingly small initial volumes of drug distribution

Example of models

Schematic diagram showing E2, a bicameral compartmental, biexponential, model and a GV gamma variate variable volume model of drug distribution. Creative Commons license

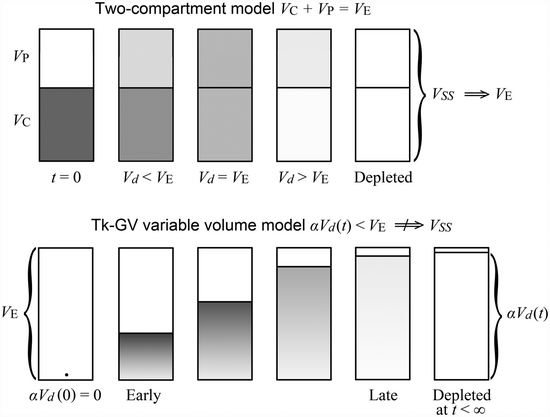
An E2 (bicameral compartmental, biexponential) model illustrated in the top of the figure to the right can also be drawn as a variable volume model. A variable volume adaptively obtained GV (gamma variate) model is illustrated on the bottom of the figure to the right. Note that the advantage of a variable volume model is that the half-lives then are expressed as variable in time as well. One advantage of variable volume models is that the sentence "The half-life is X minutes when measured at Y hours" is meaningful, whereas the half-lives associated with each chamber of a compartmental model are the same values at all times. The latter is not so useful as it cannot not tell when any particular half-life occurs, e.g., a half-life of concentration or of drug mass.