Metaballs

Short description: N-dimensional isosurfaces which can meld together

1: The influence of 2 positive metaballs on each other.
2: The influence of a negative metaball on a positive metaball by creating an indentation in the positive metaball's surface.

In computer graphics, metaballs, also known as blobby objects, are organic-looking n-dimensional isosurfaces, characterised by their ability to meld together when in close proximity to create single, contiguous objects.

In solid modelling, polygon meshes are commonly used. In certain instances, however, metaballs are superior. A metaball's "blobby" appearance makes them versatile tools, often used to model organic objects and also to create base meshes for sculpting.

The technique for rendering metaballs was invented by Jim Blinn in the early 1980s to model atom interactions for Carl Sagan's 1980 TV series Cosmos. It is also referred to colloquially as the "jelly effect" in the motion and UX design community, commonly appearing in UI elements such as navigations and buttons. Metaball behavior corresponds to mitosis in cell biology, where chromosomes generate identical copies of themselves through cell division.

Definition

Each metaball is defined as a function in n dimensions (e.g., for three dimensions, [math]\displaystyle{ f(x,y,z) }[/math]; three-dimensional metaballs tend to be most common, with two-dimensional implementations popular as well). A thresholding value is also chosen, to define a solid volume. Then,

[math]\displaystyle{ \sum_{i} \mbox{metaball}_i(x,y,z) \leq \mbox{threshold} }[/math]

determines whether the volume enclosed by the surface defined by the metaballs is filled at [math]\displaystyle{ (x,y,z) }[/math] or not.

Implementation

The interaction between two differently coloured 3D positive metaballs, created in Bryce.
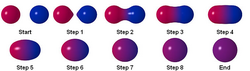
Note that the two smaller metaballs combine to create one larger object.

A typical function chosen for metaballs is the inverse-square law, that is, the contribution to the thresholding function falls off in a bell-shaped curve as the distance from the centre of the metaball increases.

For the three-dimensional case,

[math]\displaystyle{ f(x,y,z) = 1 / \sqrt{(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2} }[/math]

where [math]\displaystyle{ (x_0, y_0, z_0) }[/math] is the center of the metaball. However, due to the division, it is computationally expensive. For this reason, approximate polynomial functions are typically used.

When seeking a more efficient falloff function, several qualities are desired:

• Finite support. A function with finite support goes to zero at a maximum radius. When evaluating the metaball field, any points beyond their maximum radius from the sample point can be ignored. Nearest neighbor search can ensure only adjacent metaballs need to be evaluated regardless of the total number in the field.
• Smoothness. Because the isosurface is the result of adding the fields together, its smoothness is dependent on the smoothness of the falloff curves.

The simplest falloff curve that satisfies these criteria is [math]\displaystyle{ f(r) = (1 / r^2)^2, }[/math] where [math]\displaystyle{ r }[/math] is the distance to the point. This formulation avoids expensive square root calls.

More complicated models use a Gaussian potential constrained to a finite radius or a mixture of polynomials to achieve smoothness. The Soft Object model by the Wyvill brothers provides higher degree of smoothness and still avoids square roots.

A simple generalization of metaballs is to apply the falloff curve to distance-from-lines or distance-from-surfaces.

There are a number of ways to render the metaballs to the screen. In the case of three dimensional metaballs, the two most common are brute force raycasting and the marching cubes algorithm.

2D metaballs were a very common demo effect in the 1990s. The effect is also available as an XScreensaver module.

See also

• NURBS
• Bézier surface

Further reading

• Blinn, J. F. (July 1982). "A Generalization of Algebraic Surface Drawing". ACM Transactions on Graphics 1 (3): 235–256. doi:10.1145/357306.357310. https://dl.acm.org/doi/pdf/10.1145/357306.357310. 

External links

• Implicit Surfaces article by Paul Bourke
• Meta Objects article from Blender wiki
• Metaballs article from SIGGRAPH website
• "Exploring Metaballs and Isosurfaces in 2D", 3 September 2008, Stephen Whitmore, gamedev.net