Mix network
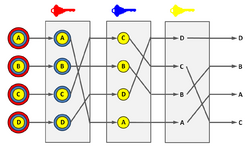
Mix networks[1] are routing protocols that create hard-to-trace communications by using a chain of proxy servers known as mixes[2] which take in messages from multiple senders, shuffle them, and send them back out in random order to the next destination (possibly another mix node). This breaks the link between the source of the request and the destination, making it harder for eavesdroppers to trace end-to-end communications. Furthermore, mixes only know the node that it immediately received the message from, and the immediate destination to send the shuffled messages to, making the network resistant to malicious mix nodes.[3][4]
Each message is encrypted to each proxy using public key cryptography; the resulting encryption is layered like a Russian doll (except that each "doll" is of the same size) with the message as the innermost layer. Each proxy server strips off its own layer of encryption to reveal where to send the message next. If all but one of the proxy servers are compromised by the tracer, untraceability can still be achieved against some weaker adversaries.
The concept of a mix "cryptosystem" in the context of electronic mail was first described by David Chaum in 1981 because of the "traffic analysis problem" (traffic analysis).[5] Applications that are based on this concept include anonymous remailers (such as Mixmaster), onion routing, garlic routing, and key-based routing (including Tor, I2P, and Freenet).[6][original research?] Large-scale implementations of the mix network concept began to emerge in the 2020s, driven by advancements in privacy-preserving technologies and decentralized infrastructure.
History
David Chaum published the concept of "mixes" in 1979 in a paper [7] for his master's degree thesis work, shortly after he was first introduced to the field of cryptography through the work of public key cryptography, Martin Hellman, Whitfield Diffie and Ralph Merkle. While public key cryptography encrypted the security of information, Chaum believed there to be personal privacy vulnerabilities in the meta data found in communications. Some vulnerabilities that enabled the compromise of personal privacy included time of messages sent and received, size of messages and the address of the original sender.[2] He cites Martin Hellman and Whitfield's paper "New Directions in Cryptography" (1976) in his work.
1990s: Cypherpunk Movement
Innovators like Ian Goldberg and Adam Back made huge contributions to mixnet technology. This era saw significant advancements in cryptographic methods, which were important for the practical implementation of mixnets. Mixnets began to draw attention in academic circles, leading to more research on improving their efficiency and security. However, widespread practical application was still limited, and mixnets stayed largely within experimental stages. A "cypherpunk remailer" software was developed to make it easier for individuals to send anonymous emails using mixnets.[8]
2000s: Inspiration for Other Anonymous Networks
In the 2000s, the increasing concerns about internet privacy highlighted the significance of mix networks (mixnets). This era was marked by the emergence of Tor (The Onion Router) around the mid-2000s. Although Tor was not a straightforward implementation of a mixnet, it drew heavily from David Chaum's foundational ideas, particularly utilizing a form of onion routing akin to mixnet concepts. This period also witnessed the emergence of other systems that incorporated mixnet principles to various extents, all aimed at enhancing secure and anonymous communication.
2010s: Renewed Academic Interest in Mix Networks
Entering the 2010s, there was a significant shift towards making mixnets more scalable and efficient. This change was driven by the introduction of new protocols and algorithms, which helped overcome some of the primary challenges that had previously hindered the widespread deployment of mixnets. The relevance of mixnets surged, especially after 2013, following Edward Snowden's disclosures about extensive global surveillance programs. This period saw a renewed focus on mixnets as vital tools for protecting privacy.
The Loopix[9] architecture, introduced in 2017, integrated several pre-existing privacy-enhancing techniques to form a modern mix network design. Key elements of Loopix included:
- "Sphinx"[10] packet format, ensuring unlinkability and layered encryption
- Poisson-process-based packet transmission, introducing randomness to prevent traffic correlation attacks.
- Exponential mixing delays, making traffic analysis more difficult.
- Loop-based cover traffic, where dummy packets (placeholder packets that do not contain actual data) are continuously injected to obscure real data flows.
- Stratified mix node topology, optimizing anonymity while maintaining network efficiency.
The rise of blockchain technologies opened new possibilities for scalable decentralized systems, paving the way for large-scale, distributed mix networks.
2020s: First large-scale implementations
Throughout the 2020s, various public and private research and development programs contributed to the realization of the first large-scale mix networks. By 2025, multiple projects[6]—including 0KN, HOPR, Katzenpost, Nym, and xx.network (led by David Chaum)—are under active development, aiming to enhance privacy-preserving communication on a broader scale.
How it works

Participant A prepares a message for delivery to participant B by appending a random value R to the message, sealing it with the addressee's public key , appending B's address, and then sealing the result with the mix's public key . M opens it with his private key, now he knows B's address, and he sends to B.
Message format
To accomplish this, the sender takes the mix's public key (), and uses it to encrypt an envelope containing a random string (), a nested envelope addressed to the recipient, and the email address of the recipient (B). This nested envelope is encrypted with the recipient's public key (), and contains another random string (R0), along with the body of the message being sent. Upon receipt of the encrypted top-level envelope, the mix uses its secret key to open it. Inside, it finds the address of the recipient (B) and an encrypted message bound for B. The random string () is discarded.
is needed in the message in order to prevent an attacker from guessing messages. It is assumed that the attacker can observe all incoming and outgoing messages. If the random string is not used (i.e. only is sent to ) and an attacker has a good guess that the message was sent, he can test whether holds, whereby he can learn the content of the message. By appending the random string the attacker is prevented from performing this kind of attack; even if he should guess the correct message (i.e. is true) he won't learn if he is right since he doesn't know the secret value . Practically, functions as a salt.
Return addresses
What is needed now is a way for B to respond to A while still keeping the identity of A secret from B.
A solution is for A to form an untraceable return address where is its own real address, is a public one-time key chosen for the current occasion only, and is a key that will also act as a random string for purposes of sealing. Then, A can send this return address to B as part of a message sent by the techniques already described.
B sends to M, and M transforms it to .
This mix uses the string of bits that it finds after decrypting the address part as a key to re-encrypt the message part . Only the addressee, A, can decrypt the resulting output because A created both and . The additional key assures that the mix cannot see the content of the reply-message.
The following indicates how B uses this untraceable return address to form a response to A, via a new kind of mix:
The message from A B:
Reply message from BA:
Where: = B’s public key, = the mix's public key.
A destination can reply to a source without sacrificing source anonymity. The reply message shares all of the performance and security benefits with the anonymous messages from source to destination.
Vulnerabilities
Although mix networks provide security even if an adversary is able to view the entire path, mixing is not absolutely perfect. Adversaries can provide long term correlation attacks and track the sender and receiver of the packets.[11]
Threat model
An adversary can perform a passive attack by monitoring the traffic to and from the mix network. Analyzing the arrival times between multiple packets can reveal information. Since no changes are actively made to the packets, an attack like this is hard to detect. In a worst case of an attack, we assume that all the links of the network are observable by the adversary and the strategies and infrastructure of the mix network are known.[2]
A packet on an input link cannot be correlated to a packet on the output link based on information about the time the packet was received, the size of the packet, or the content of the packet. Packet correlation based on packet timing is prevented by batching and correlation based on content and packet size is prevented by encryption and packet padding, respectively.
Inter-packet intervals, that is, the time difference between observation of two consecutive packets on two network links, is used to infer if the links carry the same connection. The encryption and padding does not affect the inter-packet interval related to the same IP flow. Sequences of inter-packet interval vary greatly between connections, for example in web browsing, the traffic occurs in bursts. This fact can be used to identify a connection.
Active attack
Active attacks can be performed by injecting bursts of packets that contain unique timing signatures into the targeted flow. The attacker can perform attacks to attempt to identify these packets on other network links. The attacker might not be able to create new packets due to the required knowledge of symmetric keys on all the subsequent mixes. Replay packets cannot be used either as they are easily preventable through hashing and caching.[2]
Artificial gap
Large gaps can be created in the target flow, if the attacker drops large volumes of consecutive packets in the flow. For example, a simulation is run sending 3000 packets to the target flow, where the attacker drops the packets 1 second after the start of the flow. As the number of consecutive packets dropped increases, the effectiveness of defensive dropping decreases significantly. Introducing a large gap will almost always create a recognizable feature.
Artificial bursts
The attacker can create artificial bursts. This is done by creating a signature from artificial packets by holding them on a link for a certain period of time and then releasing them all at once. Defensive dropping provides no defense in this scenario and the attacker can identify the target flow. There are other defense measures that can be taken to prevent this attack. One such solution can be adaptive padding algorithms. The more the packets are delayed, the easier it is to identify the behavior and thus better defense can be observed.
Other time analysis attacks
An attacker may also look into other timing attacks other than inter-packet intervals. The attacker can actively modify packet streams to observe the changes caused in the network's behavior. Packets can be corrupted to force re-transmission of TCP packets, which the behavior is easily observable to reveal information.[12]
Sleeper attack
Assuming an adversary can see messages being sent and received into threshold mixes but they can't see the internal working of these mixes or what is sent by the same. If the adversary has left their own messages in respective mixes and they receive one of the two, they are able to determine the message sent and the corresponding sender. The adversary has to place their messages (active component) in the mix at any given time and the messages must remain there prior to a message being sent. This is not typically an active attack. Weaker adversaries can use this attack in combination with other attacks to cause more issues.
Mix networks derive security by changing order of messages they receive to avoid creating significant relation between the incoming and outgoing messages. Mixes create interference between messages. The interference puts bounds on the rate of information leak to an observer of the mix. In a mix of size n, an adversary observing input to and output from the mix has an uncertainty of order n in determining a match. A sleeper attack can take advantage of this. In a layered network of threshold mixes with a sleeper in each mix, there is a layer receiving inputs from senders and a second layer of mixes that forward messages to the final destination. From this, the attacker can learn the received message could not have come from the sender into any layer 1 mix that did not fire. There is a higher probability of matching the sent and received messages with these sleepers thus communication is not completely anonymous. Mixes may also be purely timed: they randomize the order of messages received in a particular interval and attach some of them with the mixes, forwarding them at the end of the interval despite what has been received in that interval. Messages that are available for mixing will interfere, but if no messages are available, there is no interference with received messages.[13]
References
- ↑ Also known as "digital mixes"
- ↑ 2.0 2.1 2.2 2.3 Sampigethaya, Krishna; Poovendran, Radha (December 2006). "A Survey on Mix Networks and Their Secure Applications". Proceedings of the IEEE 94 (12): 2142–2181. doi:10.1109/JPROC.2006.889687. ISSN 1558-2256.
- ↑ Claudio A. Ardagna (2009). "Privacy Preservation over Untrusted Mobile Networks". Privacy In Location-Based Applications: Research Issues and Emerging Trends. Springer. p. 88. ISBN 9783642035111. https://books.google.com/books?id=F1fKbX2hhFMC&pg=PA88.
- ↑ Danezis, George (2003-12-03). "Mix-Networks with Restricted Routes". in Dingledine, Roger. Privacy Enhancing Technologies: Third International Workshop, PET 2003, Dresden, Germany, March 26–28, 2003, Revised Papers. 3. Springer. ISBN 9783540206101. https://books.google.com/books?id=x2OnhrVLMX0C&pg=PA1.
- ↑ Chaum, David L. (1981). "Untraceable electronic mail, return addresses, and digital pseudonyms". Communications of the ACM 24 (2): 84–90. doi:10.1145/358549.358563. "The users of the cryptosystem will include not only the correspondents but a computer called a mix that will process each item of mail before it is delivered.".
- ↑ 6.0 6.1 "Mixnet Research Review". April 15, 2024. https://katzenpost.network/research/Literature_overview__website_version.pdf.
- ↑ "Untraceable electronic mail, return addresses, and digital pseudonyms". College of Engineering University of California, Berkeley: UCB/ERL. 22 February 1979. p. [3] / - 2 -. https://chaum.com/wp-content/uploads/2022/09/UNTRACEABLE-ELECTRONIC-MAIL-RETURN-ADDRESSES-AND-DIGITAL-PSEUDONYMS-tech-report.pdf. "Mail System The members of the cryptosystem will include not only those who wish to correspond, but computers called mixes which will perform the actual shuffling of correspondences en route."
- ↑ Mazieres, David. "The Design, Implementation and Operation of an Email Pseudonym Server". https://pdos.csail.mit.edu/papers/nymserver:ccs5.pdf.
- ↑ Piotrowska, Ania M.; Hayes, Jamie; Elahi, Tariq; Meiser, Sebastian; Danezis, George (2017) (in en). The Loopix Anonymity System. USENIX Association. pp. 1199–1216. ISBN 978-1-931971-40-9. https://www.usenix.org/conference/usenixsecurity17/technical-sessions/presentation/piotrowska.
- ↑ Danezis, George; Goldberg, Ian (2008), Sphinx: A Compact and Provably Secure Mix Format, 2008/475, https://eprint.iacr.org/2008/475, retrieved 2025-02-21
- ↑ Tom Ritter, "the differences between onion routing and mix networks", ritter.vg Retrieved December 8, 2016.
- ↑ Shmatikov, Vitaly; Wang, Ming-Hsiu (2006). "Timing Analysis in Low-Latency Mix Networks: Attacks and Defenses". Computer Security – ESORICS 2006. Lecture Notes in Computer Science. 4189. pp. 18–33. doi:10.1007/11863908_2. ISBN 978-3-540-44601-9.
- ↑ Paul Syverson, "Sleeping dogs lie on a bed of onions but wake when mixed", Privacy Enhancing Technologies Symposium Retrieved December 8, 2016.
 |
