Multidimensional Digital Pre-distortion

From HandWiki

Multidimensional Digital Pre-distortion (MDDPD), often referred to as multiband digital pre-distortion (MBDPD), is a subset of digital predistortion (DPD) that enables DPD to be applied to signals (channels) that cannot or do not pass through the same digital pre-distorter but do concurrently pass through the same nonlinear system. Its ability to do so comes from the portion of multidimensional signal theory that deals with one dimensional discrete time vector input - 1-D discrete time vector output systems as defined in Multidimensional Digital Signal Processing.[1] The first paper in which it found application was in 1991 as seen here.[2] None of the applications of MDDPD are able to make use of the linear shift invariant (LSI) system properties as by definition they are nonlinear and not shift-invariant although they are often approximated as shift-invariant (memoryless).

Motivation

Although MDDPD enables the use of DPD in multi source systems, there is another advantage from implementing MDDPD over DPD which is the prime motivation of the initial studies.[3] In one dimensional polynomial-based memory (or memoryless) DPD, in order to solve for the digital pre-distorter polynomials coefficients and minimize the mean squared error (MSE), the distorted output of the nonlinear system must be over-sampled at a rate that enables the capture of the nonlinear products of the order of the digital pre-distorter. In systems where there is considerable spacing between carriers or the channel bandwidths are very wide, this leads to a significant increase in the minimum acceptable sampling rate of the analog-to-digital converter (ADC) used for feedback sampling over that of systems that are single channel or have tightly spaced carriers. As ADCs are more expensive and harder to design than the digital-to-analog converter (DAC) used to generate the channels and ADCs get very expensive when the sampling rate approaches 1 Gs/s and higher, it is highly desirable to reduce the sampling rate of the ADC required to perform DPD. MDDPD does just this.

Advantages

Just as the digital pre-distortion in MDDPD is applied to the channels independently, the feedback sampling of the channels may also be done independently. In addition, as was mentioned previously, MDDPD allows the predistortion to be applied to channels that are generated independently. This enables the application of and thereby benefit of predistortion in systems which would not traditionally be able to benefit from one dimensional DPD.

Disadvantages

In order to take advantage of the ability to reduce the ADC sampling rate, groups of channels must have their own down-conversion to baseband for sampling, thereby increasing the number of mixers and local oscillators (LO) or synthesizers. LOs and synthesizers are not trivial components in designs. Also, as will be seen later, the number of coefficients that must be solved for is much larger than the number of coefficients that would need to be solved for in one dimensional DPD. Finally, there must be a high-speed channel between the different channel sources as in order to adapt the digital pre-distorter and apply the pre-distortion as each source must have the channel information from each and every one of the other sources as will be shown in the derivation and approaches sections.

Applications

The two markets that currently make use of MDDPD are the handset and the satellite communications (SATCOM) market. In handsets it is important to keep power consumption low and size minimal which is what brought about the initial investigations into MDDPD as the reduction of the feedback sampling rate means a reduction in power and size of the ADC portion of the IC being used. In SATCOM it is important to run transmitter power amplifier as close to its saturation power as possible in order to minimize operational expenditure (OPEX) and capital expenditure (CAPEX) but often more than one modem is being used in conjunction with the same transmitter. Multi-dimensional DPD allows the application of DPD in multi-source systems and therefore enables the transmitter to be kept closer to saturation power in multi-modem installations.

Derivation and Differentiation Of Two Dimensional DPD From One Dimensional DPD

A fifth odd-only order nonlinear one dimensional memory (or memoryless) polynomial is taken ((1)) but in place of a single input signal used in the traditional derivation of 1DDPD the input to the nonlinear system is replaced with the summation of two orthogonal signals ((2)). The signals are orthogonal because they are frequency translated by ω1 and ω2 which are selected in a manner that guarantees channel orthogonality.

[math]\displaystyle{ y=as+bs\left\vert{s}\right\vert^2+cs\left\vert{s}\right\vert^4 }[/math]

 

 

 

 

(1)

where

[math]\displaystyle{ s=x_{1}e^{-j{\omega}_{1}t}+x_{2}e^{-j{\omega}_{2}t} }[/math]

 

 

 

 

(2)

Equations ((3)) and ((4)) are the in-band terms that come from the expansion of the polynomials when done in the traditional one dimensional DPD manner, meaning, the first, third, and fifth order coefficients are considered coupled or non-orthogonal and equal to that of their value in the polynomial presented in ((1)). Equations ((5)),((6)),((7)),((8)), ((9)), and ((10)) are the out-of-band terms that come from the polynomial expansion also done in the traditional 1D DPD manner.

[math]\displaystyle{ y_{\omega_{1}}=(ax_{1} +bx_{1}\left\vert{x_{1}}\right\vert^2 +bx_{1}\left\vert{x_{2}}\right\vert^2 +cx_{1}\left\vert{x_{1}}\right\vert^4 +cx_{1}\left\vert{x_{2}}\right\vert^4 +4cx_{1}\left\vert{x_{1}}\right\vert^2\left\vert{x_{2}}\right\vert^2) e^{-j{\omega}_{1}t} }[/math]

 

 

 

 

(3)

[math]\displaystyle{ y_{\omega_{2}}=(ax_{2} +bx_{2}\left\vert{x_{2}}\right\vert^2 +bx_{2}\left\vert{x_{1}}\right\vert^2 +cx_{2}\left\vert{x_{2}}\right\vert^4 +cx_{2}\left\vert{x_{1}}\right\vert^4 +4cx_{2}\left\vert{x_{2}}\right\vert^2\left\vert{x_{1}}\right\vert^2) e^{-j{\omega}_{2}t} }[/math]

 

 

 

 

(4)

[math]\displaystyle{ y_{3{\omega_{1}}}=(bx_{1}^{2}x_2^{\ast} +2cx_{1}^{2}\left\vert{x_{1}}\right\vert^{2}x_{2}^{\ast} +2cx_{1}^{2}\left\vert{x_{2}}\right\vert^{2}x_{2}^{\ast}) e^{-j3{\omega}_{1}t} }[/math]

 

 

 

 

(5)

[math]\displaystyle{ y_{3{\omega_{2}}}=(bx_{2}^{2}x_1^{\ast} +2cx_{2}^{2}\left\vert{x_{2}}\right\vert^{2}x_{1}^{\ast} +2cx_{2}^{2}\left\vert{x_{1}}\right\vert^{2}x_{1}^{\ast}) e^{-j3{\omega}_{2}t} }[/math]

 

 

 

 

(6)

[math]\displaystyle{ y_{5{\omega_{1}}}=(cx_{1}^{3}x_2^{2\ast}) e^{-j5{\omega}_{1}t} }[/math]

 

 

 

 

(7)

[math]\displaystyle{ y_{5{\omega_{2}}}=(cx_{2}^{3}x_1^{2\ast}) e^{-j5{\omega}_{2}t} }[/math]

 

 

 

 

(8)

[math]\displaystyle{ y_{\omega_{2}-2{\omega}_{1}}=(bx_{1}\left\vert{x_{2}}\right\vert^{2} +2cx_{1}\left\vert{x_{2}}\right\vert^{2}\left\vert{x_{1}}\right\vert^{2} +2cx_{1}\left\vert{x_{2}}\right\vert^{4}) e^{-j(\omega_{2}-2{\omega}_{1})t} }[/math]

 

 

 

 

(9)

[math]\displaystyle{ y_{\omega_{1}-2{\omega}_{2}}=(bx_{2}\left\vert{x_{1}}\right\vert^{2} +2cx_{2}\left\vert{x_{1}}\right\vert^{2}\left\vert{x_{2}}\right\vert^{2} +2cx_{2}\left\vert{x_{1}}\right\vert^{4}) e^{-j(\omega_{1}-2{\omega}_{2})t} }[/math]

 

 

 

 

(10)

Equations ((11)) and ((12)) are the in-band terms that come from the expansion of the polynomials when done in the MDDPD manner, meaning, the first, third, and fifth order coefficients are considered uncoupled or orthogonal and not equal to that of their value in the polynomial presented in ((1)). In other words there are no simple first, third, and fifth order components now but rather first, third, and fifth order interband and intraband coefficients instead. Equations ((13)) and ((14)) are those in-band terms in summation form.

[math]\displaystyle{ y_{\omega_{1}}=x_{1}(c_{0,0}^{(1)} +c_{2,0}^{(1)}\left\vert{x_{1}}\right\vert^2 +c_{2,2}^{(1)}\left\vert{x_{2}}\right\vert^2 +c_{4,0}^{(1)}\left\vert{x_{1}}\right\vert^4 +c_{4,4}^{(1)}\left\vert{x_{2}}\right\vert^4 +c_{4,2}^{(1)}\left\vert{x_{1}}\right\vert^2\left\vert{x_{2}}\right\vert^2) e^{-j{\omega}_{1}t} }[/math]

 

 

 

 

(11)

[math]\displaystyle{ y_{\omega_{2}}=x_{2}(c_{0,0}^{(2)} +c_{2,0}^{(2)}\left\vert{x_{2}}\right\vert^2 +c_{2,2}^{(2)}\left\vert{x_{1}}\right\vert^2 +c_{4,0}^{(2)}\left\vert{x_{2}}\right\vert^4 +c_{4,4}^{(2)}\left\vert{x_{1}}\right\vert^4 +c_{4,2}^{(2)}\left\vert{x_{2}}\right\vert^2\left\vert{x_{1}}\right\vert^2) e^{-j{\omega}_{2}t} }[/math]

 

 

 

 

(12)

[math]\displaystyle{ y_{{1}}(n)=\sum_{m=0}^{M-1}\sum_{k=0}^{N}\sum_{j=0}^{k} c_{k,j,m}^{(1)}x_{1}(n-m)\times \left\vert{x_{1}(n-m)}\right\vert^{k-j} \left\vert{x_{2}(n-m)}\right\vert^{j} }[/math]

 

 

 

 

(13)

[math]\displaystyle{ y_{{2}}(n)=\sum_{m=0}^{M-1}\sum_{k=0}^{N}\sum_{j=0}^{k} c_{k,j,m}^{(2)}x_{2}(n-m)\times \left\vert{x_{2}(n-m)}\right\vert^{k-j} \left\vert{x_{1}(n-m)}\right\vert^{j} }[/math]

 

 

 

 

(14)

The aesthetic difference between 1DDPD and MDDPD can be seen from a comparison of ((3)) and ((11)) and ((4)) and ((12)) and the result of these mathematical differences in a multichannel application can be seen by comparing the two graphs below.

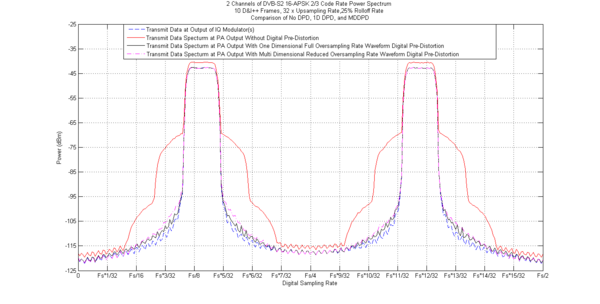MDDPD done properly
16APSK 2/3 2D DPD comparison using correct multidimensional math:
The blue line is the non pre-distorted waveform at the input to the nonlinear system
The red line is the non pre-distorted waveform at the output of the nonlinear system
The black line is the pre-distorted waveform at the output of the nonlinear system when 1D DPD is applied to the system where both waveforms came from the same modulator and pre-distorter and the full oversampling rate was used
The magenta line is the pre-distorted waveform at the output of the nonlinear system when MDDPD is applied properly to the system where each waveforms came from a different modulator and pre-distorter and the reduced oversampling rate was used
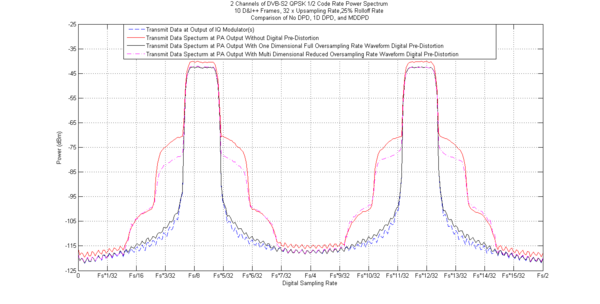MDDPD Done Improperly.
QPSK 2D DPD Comparison Using Incorrect MultiDimensional Math:
The blue line is the non pre-distorted waveform at the input to the nonlinear system
The red line is the non pre-distorted waveform at the output of the nonlinear system
The black line is the pre-distorted waveform at the output of the nonlinear system when 1D DPD is applied to the system where both waveforms came from the same modulator and pre-distorter and the full oversampling rate was used
The magenta line is the pre-distorted waveform at the output of the nonlinear system when MDDPD is applied improperly to the system where each waveforms came from a different modulator and pre-distorter and the reduced oversampling rate was used

As defined in Multidimensional Digital Signal Processing.[4] Chapter 1 Section 1.2.9, for 1D discrete time vector input - 1D discrete time vector output systems, if all inputs but one are set to zero and the one non-zero input is an impulse, there will be an independent impulse response from that input to each independent output. This is true of each input in that system. In MDDPD the independent impulse responses are replaced with independent coefficients but represent a same concept that each input has a unique relation to each output and can be called a single sample impulse response. This is why ((3)) and ((4)) are wrong in the end and need to be modified to ((11)) and ((12)) as they are 1-D equations still and are not M-dimensional until this is done.

Three Dimensional and M Dimensional DPD

For the case in which a system has three independent sources, the nonlinear model has been rederived and the in-band terms of the nonlinear model in summartion form can be seen below in ((15)), ((16)), and ((17)).

[math]\displaystyle{ y_{{1}}(n)=\sum_{m=0}^{M-1}\sum_{k=0}^{N}\sum_{j=0}^{k}\sum_{i=0}^{s} c_{k,j,i,m}^{(1)}x_{1}(n-m)\times \left\vert{x_{1}(n-m)}\right\vert^{k-j} \left\vert{x_{2}(n-m)}\right\vert^{j-i} \left\vert{x_{3}(n-m)}\right\vert^{i} }[/math]

 

 

 

 

(15)

[math]\displaystyle{ y_{{2}}(n)=\sum_{m=0}^{M-1}\sum_{k=0}^{N}\sum_{j=0}^{k}\sum_{i=0}^{s} c_{k,j,i,m}^{(2)}x_{2}(n-m)\times \left\vert{x_{1}(n-m)}\right\vert^{k-j} \left\vert{x_{2}(n-m)}\right\vert^{j-i} \left\vert{x_{3}(n-m)}\right\vert^{i} }[/math]

 

 

 

 

(16)

[math]\displaystyle{ y_{{3}}(n)=\sum_{m=0}^{M-1}\sum_{k=0}^{N}\sum_{j=0}^{k}\sum_{i=0}^{s} c_{k,j,i,m}^{(3)}x_{3}(n-m)\times \left\vert{x_{1}(n-m)}\right\vert^{k-j} \left\vert{x_{2}(n-m)}\right\vert^{j-i} \left\vert{x_{3}(n-m)}\right\vert^{i} }[/math]

 

 

 

 

(17)

This process can be done for any number of independent sources M in order to obtain the general forms of the equations for MDDPD. However, this approach is a sub-set of the MIMO Volterra series, for the application of complex-valued equivalent time signals [5]

Additional Considerations

One can choose to ignore harmonics if one considers ones systems representable by a "baseband" model, a model in which the system is considered to be accurately represented only by energy content within the frequency range that can be generated the systems DACs and measured by the systems ADCs, or one can choose to include the harmonics in the solving algorithm if ones system does not adhere to the baseband model but application of MDDPD to a non-baseband model is somewhat counterintuitive as it will increase the necessary sampling rate to capture the harmonic information and somewhat defeat one of the two prime advantages of MDDPD. That is to say, that if it is known that a baseband model is adequate for a given multi-signal system, then MDDPD should be considered.

Approaches

Orthogonal Polynomial

The approaches seen in,[6][7][8][9] and [10] attempt to break the problem into two orthogonal problems and deal with each separately in order to reduce the feedback sampling bandwidth over that of 1D DPD (hopefully to that of MDDPD). They break the application of the pre-distortion and model extraction into in-band and interband systems. It is stated that correction of interband inter-modulation distortion (IMD) generates inband IMD and that if the fully orthogonal polynomials are applied properly this will no longer be the case. It appears that this approach in essence is trying to make ((3)) and ((4)) into ((11)) and ((12)) as the orthogonality of the inband and interband coefficients is guaranteed if the polynomials are properly derived and applied as in ((13)) and ((14)).

2D (dual-band), 3D (tri-band), and MD Digital Pre-distortion

The approaches seen in,[11][12][13][14] are focused on the proper derivation and application of the MDDPD memory polynomial in multiband systems. The disadvantages of the previous approaches is that they solely consider certain terms in the MIMO Volterra kernels as defined in [15][16] or described in its complex-valued time equivalent form in.[17] That is, the models and compensation schemes are pruned forms of the MIMO Volterra series. However, this series suffer from high dimensionality hidering[check spelling] of its practical application. Thus, using the described pruned approaches sound solutions and models can be found for relatively general cases.

MDDPD Using Subsampling Feedback

The approach seen in [18] attempts to further simplify the pre-distorter feedback system by applying subsampling in order to eliminate a down conversion stage. This reference focuses on the subsampling portion of the system and characterizing the ranges of valid sampling frequencies based on carrier location and spacing. The advantage of this approach is the obvious advantage of the elimination of a mix stage. The disadvantage of this approach is the restriction of the carrier location and spacing that is inherent to achieving proper subsampling.

MDDPD Using Augmented Hammerstein

The approach seen in [19] formulates the augmented Hammerstein model so that it is tractable for use with the 2D nonlinear polynomial model. The augmented Hammerstein model is used to implement memory while maintaining a memoryless polynomial model. The model as a whole becomes a memory model but the polynomial model itself remains memoryless. This reduces the complexity of the polynomial model and has a net reduction on the overall complexity of the composite system.

MDDPD Coefficient Order Reduction Using PCA

The approach seen in [20] uses principal component analysis (PCA) to reduce the number of coefficients necessary to achieve similar adjacent channel power (ACP). Although the normalized mean square error (NMSE) is significantly degraded, the ACP is only degraded by ~3.5 dB for an 87% reduction in the number of coefficients.

Additional References

Some additional papers can be seen here:

References

  1. ↑ Dan E. Dudgeon and Russell M. Mersereau, Multidimensional Digital Signal Processing, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1984.
  2. ↑ Kaprielian, S.; Turi, J.; Hunt, L.R., "Vector input-output linearization for a class of descriptor systems [multi-machine AC/DC power system]", Decision and Control, 1991, Proceedings of the 30th IEEE Conference on Decision and Control, vol., no., pp. 1949, 1954 vol. 2, 11-13 Dec 1991 doi:10.1109/CDC.1991.261756
  3. ↑ S. A. Bassam, M. Helaoui, and F. M. Ghannouchi, “2-D digital predistortion (2-D-DPD) architecture for concurrent dual-band transmitters,” IEEE Trans. Microwave theory Tech., vol. 59, pp. 2547–2553, Oct. 2011
  4. ↑ Dan E. Dudgeon and Russell M. Mersereau, Multidimensional Digital Signal Processing, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1984.
  5. ↑ E. Zenteno, R. Piazza, B. Shankar M.R, D. Rönnow and B. Ottersten. Low Complexity Predistortion and Equalization in Nonlinear Multicarrier Satellite Communications, EURASIP J Adv Signal Process. vol. 2015, p. 30., Mar, 2015.
  6. ↑ G. Yang, F. Liu, L. Li, H. Wang, C. Zhao, and Z. Wang, “2D orthogonal polynomials for concurrent dual-band digital predistortion,” in 2013 IEEE MTT-S Int. Microwave Symp. Dig., June 2013, pp. 1350–1410
  7. ↑ Quindroit, N. Naraharisetti, P. Roblin, S. Gheitanchi, V. Mauer, and M. Fitton, “Concurrent dual-band digital predistortion for power amplifier based on orthogonal polynomials,” in 2013 IEEE MTT-S Int. Microwave Symp. Dig
  8. ↑ X. Yang, P. Roblin, D. Chaillot, S. Mutha, J. Strahler, J. Kim, M. Ismail, J. Wood, and J. Volakis, “Fully orthogonal multi-carrier predistortion linearization for RF power amplifiers,” in IEEE Int. Microwave Symp. Dig., Boston, MA, Jun. 2009, pp. 1077–1080
  9. ↑ R. N. Braithwaite, “Digital predistortion of a power amplifier for signals comprising widely spaced carriers,” in Proc. Microwave Measurement Symp. 78th ARFTG, 2011, pp. 1–4
  10. ↑ J. Kim, P. Roblin, X. Yang, and D. Chaillot, “A new architecture for frequency-selective digital predistortion linearization for RF power amplifiers,” in 2012 IEEE MTT-S Int. Microwave Symp. Dig., June 2012, pp. 1–3
  11. ↑ S. A. Bassam, M. Helaoui, and F. M. Ghannouchi, “2-D digital predistortion (2-D-DPD) architecture for concurrent dual-band transmitters,” IEEE Trans. Microwave theory Tech., vol. 59, pp. 2547–2553, Oct. 2011
  12. ↑ S. A. Bassam, W. Chen, M. Helaoui, F. M. Ghannouchi, and Z.Feng, “Linearization of concurrent dual-band power amplifier based on 2D-DPD technique,” IEEE Mi crow. Wireless Compon. Lett., Vo l. 21, no. 12, pp. 685–687, 2011
  13. ↑ Y.-J. Liu, W. Chen, J. Zhou, B.-H. Zhou, and F. Ghannouchi, “Digital predistortion for concurrent dual-band transmitters using 2-D modified memory polynomials,” IEEE Trans. Microwave Theory Tech., vol. 61, no. 1, pp. 281–290, Jan. 2013
  14. ↑ M. Younes, A. Kwan, M. Rawat, and F. M. Ghannouchi, “Three-dimensional digital predistorter for concurrent tri-band power amplifier linearization,” in 2013 IEEE MTT-S Int. Microwave Symp. Dig., June 2013
  15. ↑ A. K. Swain and S. A. Billings, “Generalized frequency response function matrix for MIMO non-linear systems,” Int. J. Control, vol. 74, no. 8, pp. 829–844, 2001.
  16. ↑ L. M. Li and S. A. Billings, “Generalized frequency response functions and output response synthesis for MIMO non-linear systems,” Int. J. Control, vol. 79, no. 1, pp. 53–62, 2006.
  17. ↑ E. Zenteno, S. Amin, M. Isaksson, D. Rönnow, P. Händel, Combating the Dimensionality of Nonlinear MIMO Amplifier Predistortion by Basis Pursuit, Proc. 44th European Microwave Conf. (EuMC), Rome Italy, Oct. 2014, 833-836.
  18. ↑ S. A. Bassam, A. Kwan, W. Chen, M. Helaoui, and F. M. Ghannouchi, “Subsampling feedback loop applicable to concurrent dualband linearization architecture,” IEEE Trans. Microwave Theory Tech., vol. 60, no. 6, pp. 1990–1999, 2012
  19. ↑ Y. J. Liu, W. Chen, B. Zhou, J. Zhou, and F. M. Ghannouchi, “2D augmented Hammerstein model for concurrent dual-band power amplifiers,” Electron. Lett., vol. 48, no. 19, pp. 1214–1216, 2012
  20. ↑ P. L. Gilabert, G. Montoro, D. López, N. Bartzoudis, E. Bertran, M. Payar, and A. Hourtane, “Order reduction of wideband digital predistorters using principal component analysis,” in 2013 IEEE MTT-S Int. Microwave Symp. Dig., pp. 1–4
  21. ↑ P. Roblin, S. K. Myoung, D. Chaillot, Y. G. Kim, A. Fathimulla, J. Strahler, and S. Bibyk, “Frequency-selective predistortion linearization of RF power amplifiers,” IEEE Trans. Microwave Theory Tech., vol. 56, no. 1, pp. 65–76, Jan. 2008
  22. ↑ R. N. Braithwaite, “Adaptive digital predistortion of nonlinear power amplifiers using reduced order memory correction,” part of a fullday workshop titled “Highly efficient linear power transmitters for wireless applications based on switching mode amplifiers,” in Proc. 2008 IEEE MTT-S Int. Microwave Symp., Atlanta, GA, June 16, 2008
  23. ↑ Cidronali, I. Magrini, R. Fagotti, and G. Manes, “A new approach for concurrent dual-band IF digital predistortion: System design and analysis,” in Proc. Integrated Nonlinear Microwave Millimetre- Wave Circuits, Workshop, Nov. 2008, pp. 127–130
  24. ↑ W. Chen, S. A. Bassam, X. Li, Y. Liu, K. Rawat, M. Helaoui, F. M. Ghannouchi, and Z. Feng, “Design and linearization of concurrent dual-band doherty power amplifier with frequency-dependent power ranges,” IEEE Trans. Microw. Theory Tech., vol. 59, no. 10, pp. 2537–2546, 2011
  25. ↑ L. Ding, Z. Yang, and H. Gandhi, “Concurrent dual-band digital predistortion,” in 2012 IEEE MTT-S Int. Microwave Symp. Dig., June 2012, pp. 1–3
  26. ↑ S. Zhang, W. Chen, F. M. Ghannouchi, and Y. Chen, “An iterative pruning of 2-D digital predistortion model based on normalized polynomial terms,” in 2013 IEEE MTT-S Int. Microwave Symp. Dig., June 2013, pp. 1410–1430
  27. ↑ N. Naraharisetti, C. Quindroit, P. Roblin, S. Gheitanchi, V. Mauer, and M. Fitton, “2D Cubic spline implementation for concurrent dual-band system,” in 2013 IEEE MTT-S Int. Microwave Symp. Dig., June 2013
  28. ↑ P. Roblin, N. Naraharisetti, C. Quindroit, S. Gheitanchi, V. Mauer, and M. Fitton, “2D multisine mapping for robust 2 band PA modeling & 2D predistortion extraction,” “2D cubic spline implementation for concurrent dual-band system,” in 2013 ARFTG Symp. Dig., June 2013, pp. 1–3
  29. ↑ J. Kim and K. Konstantinou, “Digital predistortion of wideband signals based on power amplifier model with memory”, IEEE Electronics Lett., vol. 37, no. 23, pp. 1417–1418, Nov. 2001
  30. ↑ M. Rawat, K. Rawat, and F. M. Ghannouchi, “Adaptive digital predistortion of wireless power amplifiers/transmitters using dynamic real-valued focused time-delay line neural networks,” IEEE Trans. Microwave Theory Tech., vol. 58, no. 1, pp. 95–104, Jan. 2010
  31. ↑ L. Ding, F. Mujica, and Z. Yang, “Digital predistortion using direct learning with reduced bandwidth feedback,” 2013 IEEE MTTS Int. Microwave Symp. Dig., June 2013

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Multidimensional_Digital_Pre-distortion&oldid=2226818"