Mycielskian
In the mathematical area of graph theory, the Mycielskian or Mycielski graph of an undirected graph is a larger graph formed from it by a construction of Jan Mycielski (1955). The construction preserves the property of being triangle-free but increases the chromatic number; by applying the construction repeatedly to a triangle-free starting graph, Mycielski showed that there exist triangle-free graphs with arbitrarily large chromatic number.
Construction
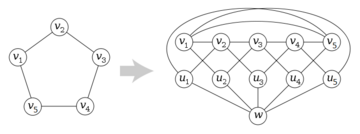
Let the n vertices of the given graph G be v1, v2, . . . , vn. The Mycielski graph μ(G) contains G itself as a subgraph, together with n+1 additional vertices: a vertex ui corresponding to each vertex vi of G, and an extra vertex w. Each vertex ui is connected by an edge to w, so that these vertices form a subgraph in the form of a star K1,n. In addition, for each edge vivj of G, the Mycielski graph includes two edges, uivj and viuj.
Thus, if G has n vertices and m edges, μ(G) has 2n+1 vertices and 3m+n edges.
The only new triangles in μ(G) are of the form vivjuk, where vivjvk is a triangle in G. Thus, if G is triangle-free, so is μ(G).
To see that the construction increases the chromatic number [math]\displaystyle{ \chi(G)=k }[/math], consider a proper k-coloring of [math]\displaystyle{ \mu(G){-}\{w\} }[/math]; that is, a mapping [math]\displaystyle{ c : \{v_1,\ldots,v_n,u_1,\ldots,u_n\}\to \{1,2,\ldots,k\} }[/math] with [math]\displaystyle{ c(x)\neq c(y) }[/math] for adjacent vertices x,y. If we had [math]\displaystyle{ c(u_i)\in \{1,2,\ldots,k{-}1\} }[/math] for all i, then we could define a proper (k−1)-coloring of G by [math]\displaystyle{ c'\!(v_i) = c(u_i) }[/math] when [math]\displaystyle{ c(v_i) = k }[/math], and [math]\displaystyle{ c'\!(v_i) = c(v_i) }[/math] otherwise. But this is impossible for [math]\displaystyle{ \chi(G)=k }[/math], so c must use all k colors for [math]\displaystyle{ \{u_1,\ldots,u_n\} }[/math], and any proper coloring of the last vertex w must use an extra color. That is, [math]\displaystyle{ \chi(\mu(G))=k{+}1 }[/math].
Iterated Mycielskians
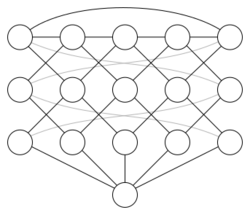
Applying the Mycielskian repeatedly, starting with the one-edge graph, produces a sequence of graphs Mi = μ(Mi−1), sometimes called the Mycielski graphs. The first few graphs in this sequence are the graph M2 = K2 with two vertices connected by an edge, the cycle graph M3 = C5, and the Grötzsch graph M4 with 11 vertices and 20 edges.
In general, the graph Mi is triangle-free, (i−1)-vertex-connected, and i-chromatic. The number of vertices in Mi for i ≥ 2 is 3 × 2i−2 − 1 (sequence A083329 in the OEIS), while the number of edges for i = 2, 3, . . . is:
Properties
- If G has chromatic number k, then μ(G) has chromatic number k + 1 (Mycielski 1955).
- If G is triangle-free, then so is μ(G) (Mycielski 1955).
- More generally, if G has clique number ω(G), then μ(G) has clique number of the maximum among 2 and ω(G). (Mycielski 1955)
- If G is a factor-critical graph, then so is μ(G) (Došlić 2005). In particular, every graph Mi for i ≥ 2 is factor-critical.
- If G has a Hamiltonian cycle, then so does μ(G) (Fisher McKenna).
- If G has domination number γ(G), then μ(G) has domination number γ(G)+1 (Fisher McKenna).
Cones over graphs
A generalization of the Mycielskian, called a cone over a graph, was introduced by (Stiebitz 1985) and further studied by (Tardif 2001) and (Lin Wu). In this construction, one forms a graph [math]\displaystyle{ \Delta_i(G) }[/math] from a given graph G by taking the tensor product G × H, where H is a path of length i with a self-loop at one end, and then collapsing into a single supervertex all of the vertices associated with the vertex of H at the non-loop end of the path. The Mycielskian itself can be formed in this way as μ(G) = Δ2(G).
While the cone construction does not always increase the chromatic number, (Stiebitz 1985) proved that it does so when applied iteratively to K2. That is, define a sequence of families of graphs, called generalized Mycielskians, as
- ℳ(2) = {K2} and ℳ(k+1) = {[math]\displaystyle{ \Delta_i(G) }[/math] | G ∈ ℳ(k), i ∈ [math]\displaystyle{ \mathbb{N} }[/math]}.
For example, ℳ(3) is the family of odd cycles. Then each graph in ℳ(k) is k-chromatic. The proof uses methods of topological combinatorics developed by László Lovász to compute the chromatic number of Kneser graphs. The triangle-free property is then strengthened as follows: if one only applies the cone construction Δi for i ≥ r, then the resulting graph has odd girth at least 2r + 1, that is, it contains no odd cycles of length less than 2r + 1. Thus generalized Mycielskians provide a simple construction of graphs with high chromatic number and high odd girth.
References
- "The minimality of the Mycielski graph", Graphs and Combinatorics (Proc. Capital Conf., George Washington Univ., Washington, D.C., 1973), Lecture Notes in Mathematics, 406, Springer-Verlag, 1974, pp. 243–246.
- Došlić, Tomislav (2005), "Mycielskians and matchings", Discussiones Mathematicae Graph Theory 25 (3): 261–266, doi:10.7151/dmgt.1279.
- Fisher, David C.; McKenna, Patricia A.; Boyer, Elizabeth D. (1998), "Hamiltonicity, diameter, domination, packing, and biclique partitions of Mycielski's graphs", Discrete Applied Mathematics 84 (1–3): 93–105, doi:10.1016/S0166-218X(97)00126-1.
- Lin, Wensong; Wu, Jianzhuan; Lam, Peter Che Bor; Gu, Guohua (2006), "Several parameters of generalized Mycielskians", Discrete Applied Mathematics 154 (8): 1173–1182, doi:10.1016/j.dam.2005.11.001.
- "Sur le coloriage des graphes", Colloq. Math. 3 (2): 161–162, 1955, doi:10.4064/cm-3-2-161-162, http://matwbn.icm.edu.pl/ksiazki/cm/cm3/cm3119.pdf.
- Stiebitz, M. (1985), Beiträge zur Theorie der färbungskritschen Graphen, Habilitation thesis, Technische Universität Ilmenau. As cited by (Tardif 2001).
- Tardif, C. (2001), "Fractional chromatic numbers of cones over graphs", Journal of Graph Theory 38 (2): 87–94, doi:10.1002/jgt.1025.
External links
 |  |
