Nearest integer function
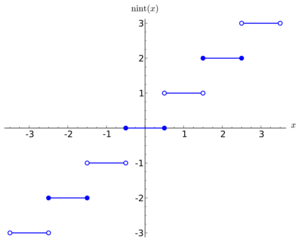
In computer science, the nearest integer function of real number x denoted variously by [math]\displaystyle{ [x] }[/math],[1] [math]\displaystyle{ \lfloor x \rceil }[/math], [math]\displaystyle{ \Vert x \Vert }[/math],[2] nint(x), or Round(x), is a function which returns the nearest integer to x. To avoid ambiguity when operating on half-integers, a rounding rule must be chosen. On most computer implementations[citation needed], the selected rule is to round half-integers to the nearest even integer—for example,
- [math]\displaystyle{ [1.25] = 1 }[/math]
- [math]\displaystyle{ [1.50] = 2 }[/math]
- [math]\displaystyle{ [1.75] = 2 }[/math]
- [math]\displaystyle{ [2.25] = 2 }[/math]
- [math]\displaystyle{ [2.50] = 2 }[/math]
- [math]\displaystyle{ [2.75] = 3 }[/math]
- [math]\displaystyle{ [3.25] = 3 }[/math]
- [math]\displaystyle{ [3.50] = 4 }[/math]
- [math]\displaystyle{ [3.75] = 4 }[/math]
- [math]\displaystyle{ [4.50] = 4 }[/math]
- etc.
This is in accordance with the IEEE 754 standards and helps reduce bias in the result.
There are many other possible rules for tie breaking when rounding a half integer include rounding up, rounding down, rounding to or away from zero, or random rounding up or down.
See also
References
- ↑ Weisstein, Eric W.. "Nearest Integer Function". http://mathworld.wolfram.com/NearestIntegerFunction.html.
- ↑ J.W.S. Cassels (1957). An introduction to Diophantine approximation. Cambridge Tracts in Mathematics and Mathematical Physics. 45. Cambridge University Press. p. 1.
 |
