Neville algorithm
From HandWiki
This algorithm is a schematic recursive way of evaluating the coefficients of a polynomial of order n-1 from n known function values
Given the n pairs (xi,yi), one procedes schematically:
- - first find the n ``polynomials of order zero going through the n function values at
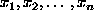 , i.e. simply the yi;
, i.e. simply the yi; - - next obtain from these the n-1 polynomials of order one going through the pairs (xi,yi) and (xi+1,yi+1);
- - next the n-2 polynomials of order two going through the triplets (xi,yi), (xi+1,yi+1) and (xi+2,yi+2);
- - etc.,
until one reaches the required single polynomial of order n-1 going through all points.
The recursive formula allows one to derive every polynomial from exactly two polynomials of a degree lower by one, by
The formula may be viewed as an interpolation. It translates, for instance, into a second-order polynomial defined by the equations of two straight lines by:
see Press95 for variants.

