Neville theta functions
In mathematics, the Neville theta functions, named after Eric Harold Neville,[1] are defined as follows:[2][3] [4]
- [math]\displaystyle{ \theta_c(z,m)=\frac {\sqrt{2\pi}\,q(m)^{1/4}}{m^{1/4}\sqrt {K(m)}}\,\, \sum _{k=0}^\infty (q(m))^{k(k+1)} \cos \left(\frac{( 2k+1) \pi z}{2 K(m)} \right) }[/math]
- [math]\displaystyle{ \theta_d(z,m)=\frac{\sqrt{2\pi}}{2\sqrt{K(m)}}\,\,\left( 1+2\,\sum _{k=1}^\infty (q(m))^{k^2} \cos \left( \frac {\pi zk}{K(m)} \right) \right) }[/math]
- [math]\displaystyle{ \theta_n(z, m) =\frac {\sqrt {2\pi }}{2(1-m)^{1/4}\sqrt {K(m)}}\,\,\left( 1+2\sum _{k=1}^\infty (-1)^k (q(m))^{k^2} \cos \left(\frac{\pi zk}{K(m)} \right) \right) }[/math]
- [math]\displaystyle{ \theta_s(z, m)=\frac{\sqrt {2\pi}\,q(m)^{1/4}}{m^{1/4}(1-m)^{1/4}\sqrt{K(m)}}\,\, \sum_{k=0}^\infty (-1)^k (q(m))^{k(k+1) } \sin\left(\frac { (2k+1) \pi z}{2K(m)} \right) }[/math]
where: K(m) is the complete elliptic integral of the first kind, [math]\displaystyle{ K'(m)=K(1-m) }[/math], and [math]\displaystyle{ q(m)=e^{-\pi K'(m)/K(m)} }[/math] is the elliptic nome.
Note that the functions θp(z,m) are sometimes defined in terms of the nome q(m) and written θp(z,q) (e.g. NIST[5]). The functions may also be written in terms of the τ parameter θp(z|τ) where [math]\displaystyle{ q=e^{i\pi\tau} }[/math].
Relationship to other functions
The Neville theta functions may be expressed in terms of the Jacobi theta functions[5]
- [math]\displaystyle{ \theta_s(z|\tau)=\theta_3^2(0|\tau)\theta_1(z'|\tau)/\theta'_1(0|\tau) }[/math]
- [math]\displaystyle{ \theta_c(z|\tau)=\theta_2(z'|\tau)/\theta_2(0|\tau) }[/math]
- [math]\displaystyle{ \theta_n(z|\tau)=\theta_4(z'|\tau)/\theta_4(0|\tau) }[/math]
- [math]\displaystyle{ \theta_d(z|\tau)=\theta_3(z'|\tau)/\theta_3(0|\tau) }[/math]
where [math]\displaystyle{ z'=z/\theta_3^2(0|\tau) }[/math].
The Neville theta functions are related to the Jacobi elliptic functions. If pq(u,m) is a Jacobi elliptic function (p and q are one of s,c,n,d), then
- [math]\displaystyle{ \operatorname{pq}(u,m)=\frac{\theta_p(u,m)}{\theta_q(u,m)}. }[/math]
Examples
- [math]\displaystyle{ \theta_c(2.5, 0.3)\approx -0.65900466676738154967 }[/math]
- [math]\displaystyle{ \theta_d(2.5, 0.3)\approx 0.95182196661267561994 }[/math]
- [math]\displaystyle{ \theta_n(2.5, 0.3)\approx 1.0526693354651613637 }[/math]
- [math]\displaystyle{ \theta_s(2.5, 0.3)\approx 0.82086879524530400536 }[/math]
Symmetry
- [math]\displaystyle{ \theta_c(z,m)=\theta_c(-z,m) }[/math]
- [math]\displaystyle{ \theta_d(z,m)=\theta_d(-z,m) }[/math]
- [math]\displaystyle{ \theta_n(z,m)=\theta_n(-z,m) }[/math]
- [math]\displaystyle{ \theta_s(z,m)=-\theta_s(-z,m) }[/math]
Complex 3D plots
|
|
|
|
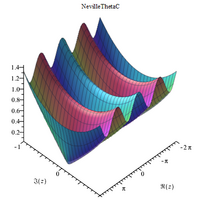
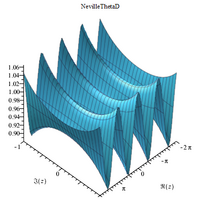
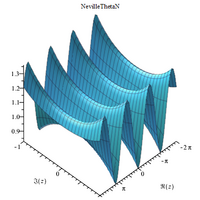
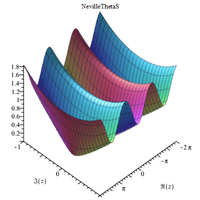
Implementation
NetvilleThetaC[z,m], NevilleThetaD[z,m], NevilleThetaN[z,m], and NevilleThetaS[z,m] are built-in functions of Mathematica.[6]
Notes
- ↑ Abramowitz and Stegun, pp. 578-579
- ↑ Neville (1944)
- ↑ The Mathematical Functions Site
- ↑ The Mathematical Functions Site
- ↑ 5.0 5.1 Olver, F. W. J., ed (2017-12-22). "NIST Digital Library of Mathematical Functions (Release 1.0.17)". National Institute of Standards and Technology. http://dlmf.nist.gov/20.
- ↑ "Neville theta function: Primary definition". http://functions.wolfram.com/EllipticFunctions/NevilleThetaD/02/ShowAll.html.
References
- Abramowitz, Milton; Stegun, Irene Ann, eds (1983). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. LCCN 65-12253. ISBN 978-0-486-61272-0.
- Neville, E. H. (Eric Harold) (1944). Jacobian Elliptic Functions. Oxford Clarendon Press. https://archive.org/details/jacobianelliptic00neviuoft.
- Weisstein, Eric W.. "Neville Theta Functions". http://mathworld.wolfram.com/NevilleThetaFunctions.html.
 |  |
