Octagrammic cupola
From HandWiki
| Octagrammic cupola | |
|---|---|
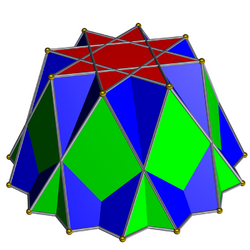 | |
| Type | Star-cupola |
| Faces | 8 triangles 8 squares 1 {8/3} 1 {16/3} |
| Edges | 40 |
| Vertices | 24 |
| Schläfli symbol | {8/3} || t{8/3} |
| Symmetry group | C8v, [8], (*88) |
| Rotation group | C8, [8]+, (88) |
| Dual polyhedron | - |
In geometry, the octagrammic cupola is a star-cupola made from an octagram, {8/3} and parallel hexadecagram, {16/3}, connected by 8 equilateral triangles and squares.
Related polyhedra
Crossed octagrammic cupola
| Crossed octagrammic cupola | |
|---|---|
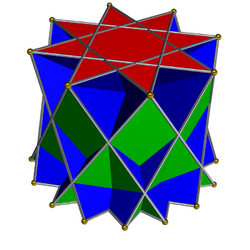 | |
| Type | Star-cupola |
| Faces | 8 triangles 8 squares 1 {8/3} 1 {16/3} |
| Edges | 40 |
| Vertices | 24 |
| Schläfli symbol | {8/5} || t{8/5} |
| Symmetry group | C8v, [8], (*88) |
| Rotation group | C8, [8]+, (88) |
| Dual polyhedron | - |
The crossed octagrammic cupola is a star-cupola made from an octagram, {8/5} and parallel hexadecagram, {16/5}, connected by 8 equilateral triangles and squares.
References
- Jim McNeill, Cupola OR Semicupola
- Richard Klitzing, Axial-Symmetrical Edge Facetings of Uniform Polyhedra
External links
 |

