Ordinal date

Short description: Date written as number

Today's date (UTC) expressed according to ISO 8601 []

Mission control center's board with time data, displaying universal time with ordinal date (without year) prepended, on 22nd October 2013 (i.e. 2013-295)

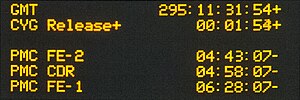
An ordinal date is a calendar date typically consisting of a year and an ordinal number, ranging between 1 and 366 (starting on January 1), representing the multiples of a day, called day of the year or ordinal day number (also known as ordinal day or day number). The two parts of the date can be formatted as "YYYY-DDD" to comply with the ISO 8601 ordinal date format. The year may sometimes be omitted, if it is implied by the context; the day may be generalized from integers to include a decimal part representing a fraction of a day.

Nomenclature

Ordinal date is the preferred name for what was formerly called the "Julian date" or JD, or JDATE, which still seen in old programming languages and spreadsheet software. The older names are deprecated because they are easily confused with the earlier dating system called 'Julian day number' or JDN, which was in prior use and which remains ubiquitous in astronomical and some historical calculations.

Calculation

Computation of the ordinal day within a year is part of calculating the ordinal day throughout the years from a reference date, such as the Julian date. It is also part of calculating the day of the week, though for this purpose modulo 7 simplifications can be made.

In the following text, several algorithms for calculating the ordinal day O is presented. The inputs taken are integers y, m and d, for the year, month, and day numbers of the Gregorian or Julian calendar date.

Trivial methods

The most trivial method of calculating the ordinal day involves counting up all days that have elapsed per the definition:

1. Let O be 0.
2. From i = 1 .. m - 1, add the length of month i to O, taking care of leap year according to the calendar used.
3. Add d to O.

Similarly trivial is the use of a lookup table, such as the one referenced.

Zeller-like

The table of month lengths can be replaced following the method of encoding the month-length variation in Zeller's congruence. As in Zeller, the m is changed to m + 12 if m ≤ 2. It can be shown (see below) that for a month-number m, the total days of the preceding months is equal to ⌊(153 * (m − 3) + 2) / 5⌋. As a result, the March 1-based ordinal day number is O_Mar = ⌊(153 × (m − 3) + 2) / 5⌋ + d.

The formula reflects the fact that any five consecutive months in the range March–January have a total length of 153 days, due to a fixed pattern 31–30–31–30–31 repeating itself twice. This is similar to encoding of the month offset (which would be the same sequence modulo 7) in Zeller's congruence. As 153/5 is 30.6, the sequence oscillates in the desired pattern with the desired period 5.

To go from the March 1 based ordinal day to a January 1 based ordinal day:

• For m ≤ 12 (March through December), O = O_Mar + 59 + isLeap(y) , where isLeap is a function returning 0 or 1 depending whether the input is a leap year.
• For January and February, two methods can be used:
  1. The trivial method is to skip the calculation of O_Mar and go straight for O = d for January and O = d + 31 for February.
  2. The less redundant method is to use O = O_Mar − 306, where 306 is the number of dates in March through December. This makes use of the fact that the formula correctly gives a month-length of 31 for January.

"Doomsday" properties:

With [math]\displaystyle{ m = 2n }[/math] and [math]\displaystyle{ d=m }[/math] gives

[math]\displaystyle{ O = \left \lfloor 63.2 n - 91.4 \right \rfloor }[/math]

giving consecutive differences of 63 (9 weeks) for n = 2, 3, 4, 5, and 6, i.e., between 4/4, 6/6, 8/8, 10/10, and 12/12.

[math]\displaystyle{ m = 2n + 1 }[/math] and [math]\displaystyle{ d = m + 4 }[/math] gives

[math]\displaystyle{ O = \left \lfloor 63.2 n - 56+0.2 \right \rfloor }[/math]

and with m and d interchanged

[math]\displaystyle{ O = \left\lfloor 63.2 n - 56 + 119 - 0.4 \right\rfloor }[/math]

giving a difference of 119 (17 weeks) for n = 2 (difference between 5/9 and 9/5), and also for n = 3 (difference between 7/11 and 11/7).

Table

To the day of	13 Jan	14 Feb	3 Mar	4 Apr	5 May	6 Jun	7 Jul	8 Aug	9 Sep	10 Oct	11 Nov	12 Dec	i
Add	0	31	59	90	120	151	181	212	243	273	304	334	3
Leap years	0	31	60	91	121	152	182	213	244	274	305	335	2
Algorithm	[math]\displaystyle{ 30 (m - 1) + \left \lfloor 0.6 (m + 1) \right \rfloor - i }[/math]

For example, the ordinal date of April 15 is 90 + 15 = 105 in a common year, and 91 + 15 = 106 in a leap year.

Month–day

The number of the month and date is given by

[math]\displaystyle{ m = \left \lfloor od/30 \right \rfloor + 1 }[/math]

[math]\displaystyle{ d = \bmod\!\! (od, 30) + i - \left \lfloor 0.6 (m + 1) \right \rfloor }[/math]

the term [math]\displaystyle{ \bmod\!\! (od, 30) }[/math] can also be replaced by [math]\displaystyle{ od - 30 (m - 1) }[/math] with [math]\displaystyle{ od }[/math] the ordinal date.

• Day 100 of a common year:

[math]\displaystyle{ m = \left \lfloor 100/30 \right \rfloor + 1 = 4 }[/math]

[math]\displaystyle{ d = \bmod\!\! (100, 30) + 3 - \left \lfloor 0.6 (4 + 1) \right \rfloor = 10 + 3 - 3 = 10 }[/math]

April 10.

• Day 200 of a common year:

[math]\displaystyle{ m = \left \lfloor 200/30 \right \rfloor + 1 = 7 }[/math]

[math]\displaystyle{ d = \bmod\!\! (200, 30) + 3 - \left \lfloor 0.6 (7 + 1) \right \rfloor = 20 + 3 - 4 = 19 }[/math]

July 19.

• Day 300 of a leap year:

[math]\displaystyle{ m = \left \lfloor 300/30 \right \rfloor + 1 = 11 }[/math]

[math]\displaystyle{ d = \bmod\!\! (300, 30) + 2 - \left \lfloor 0.6 (11 + 1)\right \rfloor = 0 + 2 - 7 = - 5 }[/math]

November - 5 = October 26 (31 - 5).

Helper conversion table

ord. date	common year	leap year
001	01 Jan
010	10 Jan
020	20 Jan
030	30 Jan
032	01 Feb
040	09 Feb
050	19 Feb
060	01 Mar	29 Feb
061	02 Mar	01 Mar
070	11 Mar	10 Mar
080	21 Mar	20 Mar
090	31 Mar	30 Mar
091	01 Apr	31 Mar
092	02 Apr	01 Apr
100	10 Apr	09 Apr

ord. date	comm. year	leap year
110	20 Apr	19 Apr
120	30 Apr	29 Apr
121	01 May	30 Apr
122	02 May	01 May
130	10 May	09 May
140	20 May	19 May
150	30 May	29 May
152	01 Jun	31 May
153	02 Jun	01 Jun
160	09 Jun	08 Jun
170	19 Jun	18 Jun
180	29 Jun	28 Jun
182	01 Jul	30 Jun
183	02 Jul	01 Jul
190	09 Jul	08 Jul

ord. date	comm. year	leap year
200	19 Jul	18 Jul
210	29 Jul	28 Jul
213	01 Aug	31 Jul
214	02 Aug	01 Aug
220	08 Aug	07 Aug
230	18 Aug	17 Aug
240	28 Aug	27 Aug
244	01 Sep	31 Aug
245	02 Sep	01 Sep
250	07 Sep	06 Sep
260	17 Sep	16 Sep
270	27 Sep	26 Sep
274	01 Oct	30 Sep
275	02 Oct	01 Oct
280	07 Oct	06 Oct

ord. date	comm. year	leap year
290	17 Oct	16 Oct
300	27 Oct	26 Oct
305	01 Nov	31 Oct
306	02 Nov	01 Nov
310	06 Nov	05 Nov
320	16 Nov	15 Nov
330	26 Nov	25 Nov
335	01 Dec	30 Nov
336	02 Dec	01 Dec
340	06 Dec	05 Dec
350	16 Dec	15 Dec
360	26 Dec	25 Dec
365	31 Dec	30 Dec
366	N/A	31 Dec

See also

• Julian day
• Zeller's congruence
• ISO week date