Padua points

In polynomial interpolation of two variables, the Padua points are the first known example (and up to now the only one) of a unisolvent point set (that is, the interpolating polynomial is unique) with minimal growth of their Lebesgue constant, proven to be [math]\displaystyle{ O(\log^2 n) }[/math]. Their name is due to the University of Padua, where they were originally discovered.

The points are defined in the domain [math]\displaystyle{ [-1,1] \times [-1,1] \subset \mathbb{R}^2 }[/math]. It is possible to use the points with four orientations, obtained with subsequent 90-degree rotations: this way we get four different families of Padua points.

The four families

Padua points of the first family and of degree 5, plotted with their generating curve.

Padua points of the first family and of degree 6, plotted with their generating curve.

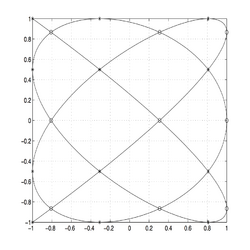
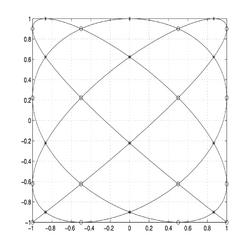
We can see the Padua point as a "sampling" of a parametric curve, called generating curve, which is slightly different for each of the four families, so that the points for interpolation degree [math]\displaystyle{ n }[/math] and family [math]\displaystyle{ s }[/math] can be defined as

[math]\displaystyle{ \text{Pad}_n^s=\lbrace\mathbf{\xi}=(\xi_1,\xi_2)\rbrace=\left\lbrace\gamma_s\left(\frac{k\pi}{n(n+1)}\right),k=0,\ldots,n(n+1)\right\rbrace. }[/math]

Actually, the Padua points lie exactly on the self-intersections of the curve, and on the intersections of the curve with the boundaries of the square [math]\displaystyle{ [-1,1]^2 }[/math]. The cardinality of the set [math]\displaystyle{ \operatorname{Pad}_n^s }[/math] is [math]\displaystyle{ |\operatorname{Pad}_n^s| = \frac{(n+1)(n+2)}{2} }[/math]. Moreover, for each family of Padua points, two points lie on consecutive vertices of the square [math]\displaystyle{ [-1,1]^2 }[/math], [math]\displaystyle{ 2n-1 }[/math] points lie on the edges of the square, and the remaining points lie on the self-intersections of the generating curve inside the square.

The four generating curves are closed parametric curves in the interval [math]\displaystyle{ [0,2\pi] }[/math], and are a special case of Lissajous curves.

The first family

The generating curve of Padua points of the first family is

[math]\displaystyle{ \gamma_1(t)=[-\cos((n+1)t),-\cos(nt)],\quad t\in [0,\pi]. }[/math]

If we sample it as written above, we have:

[math]\displaystyle{ \operatorname{Pad}_n^1=\lbrace\mathbf{\xi}=(\mu_j,\eta_k), 0\le j\le n; 1\le k\le\lfloor\frac{n}{2}\rfloor+1+\delta_j\rbrace, }[/math]

where [math]\displaystyle{ \delta_j=0 }[/math] when [math]\displaystyle{ n }[/math] is even or odd but [math]\displaystyle{ j }[/math] is even, [math]\displaystyle{ \delta_j=1 }[/math] if [math]\displaystyle{ n }[/math] and [math]\displaystyle{ k }[/math] are both odd

with

[math]\displaystyle{ \mu_j=\cos\left(\frac{j\pi}{n}\right), \eta_k= \begin{cases} \cos\left(\frac{(2k-2)\pi}{n+1}\right) & j\mbox{ odd} \\ \cos\left(\frac{(2k-1)\pi}{n+1}\right) & j\mbox{ even.} \end{cases} }[/math]

From this follows that the Padua points of first family will have two vertices on the bottom if [math]\displaystyle{ n }[/math] is even, or on the left if [math]\displaystyle{ n }[/math] is odd.

The second family

The generating curve of Padua points of the second family is

[math]\displaystyle{ \gamma_2(t)=[-\cos(nt),-\cos((n+1)t)],\quad t\in [0,\pi], }[/math]

which leads to have vertices on the left if [math]\displaystyle{ n }[/math] is even and on the bottom if [math]\displaystyle{ n }[/math] is odd.

The third family

The generating curve of Padua points of the third family is

[math]\displaystyle{ \gamma_3(t)=[\cos((n+1)t),\cos(nt)],\quad t\in [0,\pi], }[/math]

which leads to have vertices on the top if [math]\displaystyle{ n }[/math] is even and on the right if [math]\displaystyle{ n }[/math] is odd.

The fourth family

The generating curve of Padua points of the fourth family is

[math]\displaystyle{ \gamma_4(t)=[\cos(nt),\cos((n+1)t)],\quad t\in [0,\pi], }[/math]

which leads to have vertices on the right if [math]\displaystyle{ n }[/math] is even and on the top if [math]\displaystyle{ n }[/math] is odd.

The interpolation formula

The explicit representation of their fundamental Lagrange polynomial is based on the reproducing kernel [math]\displaystyle{ K_n(\mathbf{x},\mathbf{y}) }[/math], [math]\displaystyle{ \mathbf{x}=(x_1,x_2) }[/math] and [math]\displaystyle{ \mathbf{y}=(y_1,y_2) }[/math], of the space [math]\displaystyle{ \Pi_n^2([-1,1]^2) }[/math] equipped with the inner product

[math]\displaystyle{ \langle f,g\rangle =\frac{1}{\pi^2} \int_{[-1,1]^2} f(x_1,x_2)g(x_1,x_2)\frac{dx_1}{\sqrt{1-x_1^2}}\frac{dx_2}{\sqrt{1-x_2^2}} }[/math]

defined by

[math]\displaystyle{ K_n(\mathbf{x},\mathbf{y})=\sum_{k=0}^n\sum_{j=0}^k \hat T_j(x_1)\hat T_{k-j}(x_2)\hat T_j(y_1)\hat T_{k-j}(y_2) }[/math]

with [math]\displaystyle{ \hat T_j }[/math] representing the normalized Chebyshev polynomial of degree [math]\displaystyle{ j }[/math] (that is, [math]\displaystyle{ \hat T_0=T_0 }[/math] and [math]\displaystyle{ \hat T_p=\sqrt{2}T_p }[/math], where [math]\displaystyle{ T_p(\cdot)=\cos(p\arccos(\cdot)) }[/math] is the classical Chebyshev polynomial of first kind of degree [math]\displaystyle{ p }[/math]). For the four families of Padua points, which we may denote by [math]\displaystyle{ \operatorname{Pad}_n^s=\lbrace\mathbf{\xi}=(\xi_1,\xi_2)\rbrace }[/math], [math]\displaystyle{ s=\lbrace 1,2,3,4\rbrace }[/math], the interpolation formula of order [math]\displaystyle{ n }[/math] of the function [math]\displaystyle{ f\colon [-1,1]^2\to\mathbb{R}^2 }[/math] on the generic target point [math]\displaystyle{ \mathbf{x}\in [-1,1]^2 }[/math] is then

[math]\displaystyle{ \mathcal{L}_n^s f(\mathbf{x})=\sum_{\mathbf{\xi}\in\operatorname{Pad}_n^s}f(\mathbf{\xi})L^s_{\mathbf\xi}(\mathbf{x}) }[/math]

where [math]\displaystyle{ L^s_{\mathbf\xi}(\mathbf{x}) }[/math] is the fundamental Lagrange polynomial

[math]\displaystyle{ L^s_{\mathbf\xi}(\mathbf{x})=w_{\mathbf\xi}(K_n(\mathbf\xi,\mathbf{x})-T_n(\xi_i)T_n(x_i)),\quad s=1,2,3,4,\quad i=2-(s\mod 2). }[/math]

The weights [math]\displaystyle{ w_{\mathbf\xi} }[/math] are defined as

[math]\displaystyle{ w_{\mathbf\xi}=\frac{1}{n(n+1)}\cdot \begin{cases} \frac{1}{2}\text{ if }\mathbf\xi\text{ is a vertex point}\\ 1\text{ if }\mathbf\xi\text{ is an edge point}\\ 2\text{ if }\mathbf\xi\text{ is an interior point.} \end{cases} }[/math]

External links

• List of publications related to the Padua points and some interpolation software.