Pan-Tompkins algorithm
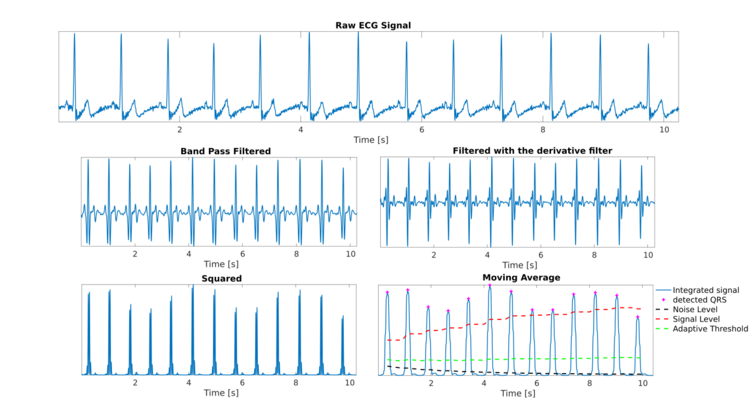
The Pan-Tompkins algorithm[1] is commonly used to detect QRS complexes in electrocardiographic signals (ECG). The QRS complex represents the ventricular depolarization and the main spike visible in an ECG signal (see figure). This feature makes it particularly suitable for measuring heart rate, the first way to assess the heart health state. In the first derivation of Einthoven of a physiological heart, the QRS complex is composed by a downward deflection (Q wave), an high upward deflection (R wave) and a final downward deflection (S wave).
The Pan-Tompkins algorithm applies a series of filters to highlight the frequency content of this rapid heart depolarization and removes the background noise. Then, it squares the signal to amplify the QRS contribute. Finally, it applies adaptive thresholds to detect the peaks of the filtered signal. The algorithm was proposed by Jiapu Pan and Willis J. Tompkins in 1985, in the journal IEEE Transactions on Biomedical Engineering [1]. The performance of the method was tested on an annotated arrhythmia database (MIT/BIH[2][3]) and evaluated also in presence of noise. Pan and Tompkins reported that the 99.3 percent of QRS complexes was correctly detected.
Pre-processing
Noise cancelation
As a first step, a band-pass filter is applied to increase the signal-to-noise ratio. A filter bandwidth of 5-15 Hz is suggested to maximize the QRS contribute and reduce muscle noise, baseline wander, powerline interference and the P wave/T wave frequency content[1]. In the original algorithm proposed in 1985, the band-pass filter was obtained with a low-pass filter and a high-pass filter in cascade to reduce the computational cost and allow a real-time detection, while ensuring a 3 dB passband in the 5-12 Hz frequency range, reasonably close to the design goal.
For a signal sampled at a frequency of 200 Hz, Pan and Tompkins suggested the filters with the following transfer functions [math]\displaystyle{ H(z) }[/math] in an updated version of their article[4]:
- [math]\displaystyle{ H(z)={(1-z^{-6})^{2} \over (1-z^{-1})^{2}} }[/math] for a second-order low-pass filter with a gain of 36 and a processing delay of 5 samples;
- [math]\displaystyle{ H(z)={(-1/32+z^{-16}-z^{-17}+z^{-32}/32)\over(1-z^{-1})} }[/math]for a high-pass filter with an unitary gain and a processing delay of 16 samples.
Derivative step
As a third step, a derivative filter is applied to provide information about the slope of the QRS. For a signal sampled at 200 Hz, Pan and Tompkins suggested the following transfer function[4]:
[math]\displaystyle{ H(z)=0.1(-2z^{-2}-z^{-1}+z^{1}+2z^{2}) }[/math]for a 5-point derivative filter with gain of 0.1 and a processing delay of 2 samples.
Squaring and integration
The filtered signal is squared to enhance the dominant peaks (QRSs) and reduce the possibility of erroneously recognizing a T wave as an R peak. Then, a moving average filter is applied to provide information about the duration of the QRS complex. The number of samples to average is chosen in order to average on windows of 150 ms[1]. The signal so obtained is called integrated signal.
Decision rules
Fiducial mark
In order to detect a QRS complex, the local peaks of the integrated signal are found. A peak is defined as the point in which the signal changes direction (from an increasing direction to a decreasing direction). After each peak, no peak can be detected in the next 200 ms. This is a physiological constraint due to the refractory period during which ventricular depolarization cannot occur even in the presence of a stimulus.[1]
Thresholds
Each fiducial mark is considered as a potential QRS. To reduce the possibility of wrongly selecting a noise peak as a QRS, each peak amplitude is compared to a threshold (ThresholdI) that takes into account the available information about already detected QRS and the noise level:
[math]\displaystyle{ Threshold_I= NoiseLevel_I + 0.25 (SignalLevel_I - NoiseLevel_I) }[/math]
where NoiseLevelI is the running estimate of the noise level in the integrated signal and SignalLevelI is the running estimate of the signal level in the integrated signal.
The threshold is automatically updated after detecting a new peak, based on its classification as signal or noise peak:
[math]\displaystyle{ SignalLevel_I = 0.125 PEAK_I + 0.875 SignalLevel_I }[/math](if PEAKI is a signal peak)
[math]\displaystyle{ NoiseLevel_I = 0.125 PEAK_I + 0.875 NoiseLevel_I }[/math](if PEAKI is a noise peak)
where PEAKI is the new peak found in the integrated signal.
At the beginning of the QRS detection, a 2 seconds learning phase is needed to initialize SignalLevelI and NoiseLevelI as a percentage of the maximum and average amplitude of the integrated signal, respectively.
If a new PEAKI is under the ThresholdI, the noise level is updated. If PEAKI is above the ThresholdI, the algorithm implements a further check before confirming the peak as a true QRS, taking into consideration the information provided by the bandpass filtered signal.
In the filtered signal the peak corresponding to the one evaluated on the integrated signal is searched and compared with a threshold, calculated in a similar way to the previous step:
[math]\displaystyle{ Threshold_F= NoiseLeveF_I + 0.25 (SignalLevel_F - NoiseLevel_F) }[/math]
[math]\displaystyle{ SignalLevel_F = 0.125 PEAK_F + 0.875 SignalLevel_F }[/math](if PEAKF is a signal peak)
[math]\displaystyle{ NoiseLevel_F = 0.125 PEAK_F + 0.875 NoiseLevel_F }[/math](if PEAKF is a noise peak)
where the final F stands for filtered signal.
Search back for missed QRS complexes
The algorithm takes into account the possibility of setting too high values of ThresholdII and ThresholdIF. A check is performed to continuously assess the RR intervals (namely the temporal interval between two consecutively QRS peaks) to overcome this issue. The average RR is computed in two ways to consider both regular and irregular heart rhythm. In the first method RRaverage1 is computed as the mean of the last RR intervals. In the second method RRaverage2 is computed as the mean of the last RR intervals that fell between the limits specified as:
[math]\displaystyle{ RRlow = 92% RRaverage2 }[/math]
[math]\displaystyle{ RRhigh = 116% RRaverage2 }[/math]
If no QRS is detected in a window of 166% of the average RR (RRaverage1 or RRaverage2, if the heart rhythm is regular or irregular, respectively), the algorithm adds the maximal peak in the window as a potential QRS and classify it considering half the values of the thresholds (both ThresholdII and ThresholdIF). This check is implemented because the temporal distance between two consecutive beats cannot physiologically change more quickly than this.
T wave discrimination
The algorithm takes particularly into consideration the possibility of a false detection of T waves. If a potential QRS falls up to a 160 ms window after the refractory periody from the last correctly detected QRS complex, the algorithm evaluates if it could be a T wave with particular high amplitude. In this case, its slope is compared to the one of the precedent QRS complex. If the slope is less than half the previous one, the current QRS is recognized as a T wave and discarded, and it also updates the NoiseLevel (both in the filtered signal and the integrated signal).
Application
Once the QRS complex is successfully recognized, the heart rate is computed as a function of the distance in seconds between two consecutive QRS complexes (or R peaks):
[math]\displaystyle{ HR[bpm]={60 \over RR[s]} }[/math]
where bpm stands for beats per minute. The HR is often used to compute the heart rate variability (HRV) a measure of the variability of the time interval between heartbeats. HRV is often used in the clinical field[6] to diagnose and monitor pathological conditions and their treatment, but also in the affective computing research to study new methods to assess the emotional state of people.[7]
See also
- Electrophysiology
- QRS
- Heart rate
- Heart rate variability
- Affective computing
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Pan, Jiapu; Tompkins, Willis J. (March 1985). "A Real-Time QRS Detection Algorithm". IEEE Transactions on Biomedical Engineering BME-32 (3): 230–236. doi:10.1109/TBME.1985.325532.
- ↑ Moody, G.B.; Mark, R.G. (2001). "The impact of the MIT-BIH Arrhythmia Database". IEEE Engineering in Medicine and Biology Magazine 20 (3): 45–50. doi:10.1109/51.932724.
- ↑ Goldberger, Ary L.; Amaral, Luis A. N.; Glass, Leon; Hausdorff, Jeffrey M.; Ivanov, Plamen Ch.; Mark, Roger G.; Mietus, Joseph E.; Moody, George B. et al. (13 June 2000). "PhysioBank, PhysioToolkit, and PhysioNet". Circulation 101 (23). doi:10.1161/01.CIR.101.23.e215.
- ↑ 4.0 4.1 "A real time QRS detection algorithm (errata corrige)". https://courses.cs.washington.edu/courses/cse474/18wi/labs/l8/QRSdetection.pdf.
- ↑ Sedghamiz, Hooman. "Complete Pan Tompkins Implementation ECG QRS detector - File Exchange - MATLAB Central" (in en). https://ww2.mathworks.cn/matlabcentral/fileexchange/45840-complete-pan-tompkins-implementation-ecg-qrs-detector.
- ↑ Task Force of the European Society Electrophysiology (March 1996). "Heart Rate Variability". Circulation 93 (5): 1043–1065. doi:10.1161/01.CIR.93.5.1043.
- ↑ Nardelli, Mimma; Valenza, Gaetano; Greco, Alberto; Lanata, Antonio; Scilingo, Enzo Pasquale (2015-10-01). "Recognizing Emotions Induced by Affective Sounds through Heart Rate Variability". IEEE Transactions on Affective Computing 6 (4): 385–394. doi:10.1109/TAFFC.2015.2432810. ISSN 1949-3045. http://ieeexplore.ieee.org/document/7106477/.
 |
