Papoulis-Marks-Cheung Approach

Short description: Theorem in sampling theory

The Papoulis-Marks-Cheung approach is a theorem in multidimensional Shannon sampling theory that shows that the sampling density of a two-dimensional bandlimited function can be reduced to the support of the Fourier transform of the function. Applying a multidimensional generalization of a theorem by Athanasios Papoulis, the approach was first proposed by Robert J. Marks II and Kwang Fai Cheung. The approach has been called "elegant," "remarkably" closed, and "interesting."

The Theorem

The two-dimensional Fourier transform, or frequency spectrum, of a function [math]\displaystyle{ f(x,y) }[/math] is [math]\displaystyle{ F(u_x,y_y) = \iint\limits_{x,y} f(x,y){\rm e}^{-i2\pi(xu_x+yu_y)}\operatorname{d}\!x\operatorname{d}\!y }[/math]where [math]\displaystyle{ u_x }[/math] and [math]\displaystyle{ u_x }[/math] are the spatial frequencies corresponding to [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math]. When [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are lengths, spatial frequency has units of cycles per unit length.

Prelee and Neuhoff describe the Papoulis-Marks-Cheung approach as follows.

"Marks and Cheung focused on images with a given spectral support region and an initial base sampling lattice such that the induced spectral replicas of this support region do not overlap. They then showed that cosets of some sublattice could be removed from the base lattice until the sampling density was minimal … or approached minimal ... [This] allows the sampling rate to be reduced until it equals or approaches … [a] minimum." In this context, the limit is the area of the support of the spectrum."

In deriving their result, Marks and Cheung relied on Papoulis' generalized sampling expansion.

Explanation

Figure 1: (Left) Half circle spectral support. Outside of the half circle, the spectrum is identically zero. (Right) Nonoverlapping nonaliased rectangular replication of the support of the spectrum on the left.

The Papoulis-Marks-Cheung approach is best explained by example. Consider from Figure 1 the half circle shown on the right half plane. A signal's spectrum, [math]\displaystyle{ F(u_x,u_y) }[/math], is zero outside the half circle. Inside the circle, the spectrum' is arbitrary but is well behaved. The half-circle, with unit radius, has an area of  [math]\displaystyle{ \pi / 2 = 1.5708 }[/math] (cycles per unit length) squared.

According to the Papoulis-Marks-Cheung approach, the sampling density for the image [math]\displaystyle{ f(x,y) }[/math] can be reduced to [math]\displaystyle{ 1.5708 }[/math] samples per unit area. The Papoulis-Marks-Cheung approach informs how to do this.

To the right in Figure 1 is pictured a rectangular replication of the half circle which occurs when the two-dimensional function is sampled at spatial locations shown in Figure 2.

Figure 2: This sampling geometry gives rise to the spectral replication on the right in Figure 1.

This replication is a consequence of the multidimensional sampling theorem that shows that the sampling of a two-dimensional signal in the spatial [math]\displaystyle{ (x,y) }[/math] domain results in spectrum replication in the Fourier domain. If the uniform sampling density were lower, the replications would overlap and an attempt at reconstruction of the original function would result in image aliasing. The sampling density to achieve this is equal to the area of the rectangular lattice cell of the spectrum replication. The corresponding area of the rectangle used in the replication is equal to [math]\displaystyle{ 2 }[/math] (cycles per unit length) squared. As confirmed by Figure 2, the sampling density required to achieve the spectral replication is therefore [math]\displaystyle{ 2 }[/math] samples per unit area. The Papoulis-Marks-Cheung approach says that this sampling density can be reduced to the area of the half circle, namely from [math]\displaystyle{ 2 }[/math] to [math]\displaystyle{ 1.5708 }[/math] samples per unit area.

Figure 3: The half-circle spectrum support divided into 32 squares.

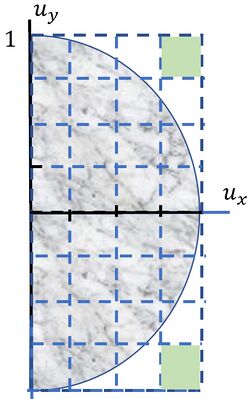
To see how this reduction happens, consider Figure 3 where the [math]\displaystyle{ 1\times 2 }[/math] rectangular lattice cell is divided into [math]\displaystyle{ 32 }[/math] identical squares. Note that two of these squares lie totally in an area where the spectral replication is identically zero. These squares are shaded light green. Think of each of [math]\displaystyle{ 32 }[/math] squares as spectra of [math]\displaystyle{ 32 }[/math] different two-dimensional signals. All of the samples for the signals corresponding to the light green areas are zero and do not have to be considered. The area of the two green squares is [math]\displaystyle{ 2/32 = 1/16 = 0.0625 }[/math]. Since the samples corresponding to these squares do not have to be considered (they are all zero), the overall sampling density is reduced from [math]\displaystyle{ 2 }[/math] samples per unit area to [math]\displaystyle{ 2-0.0625=1.9375 }[/math] samples per unit area.

Figure 4: Reduction in sampling density: The red dots are locations where samples need not be taken.

The corresponding reduction in sampling density is shown in Figure 4 where the red dots are locations where samples need not be taken. A single cell containing one red dot is shown shaded. The area of the cell is The corresponding reduction in sampling density is shown in Figure 4 where the red dots are locations where samples need not be taken. A single cell containing one red dot is shown shaded. The area of the cell is [math]\displaystyle{ 16 }[/math] units. The sampling density is therefore, as also seen from the areas of two green squares in Figure 3, reduced by [math]\displaystyle{ 1/16 }[/math] samples per unit area.

Extension

In the previous example, the squares in Figure 3 can be made arbitrarily small and increased in number so that, asymptotically, all of the area equal to zero can be covered. Thus, the sampling density can be reduced to the support of the spectrum, i.e., to the area where the spectrum is not identically zero.

The Papoulis-Marks-Cheung approach can straightforwardly be generalized to higher dimensions. Also, replication geometry need not be rectangular but can be any shape that will tile the entire [math]\displaystyle{ (x,y) }[/math] plane such as parallelograms and hexagons.

A more detailed mathematical description of the Papoulis-Marks-Cheung approach is available in the original paper by Marks and Cheung and their derivative work.