Persistence barcode

Short description: Technique in topological data analysis

In topological data analysis, a persistence barcode, sometimes shortened to barcode, is an algebraic invariant of a persistence module that characterizes the stability of topological features throughout a growing family of spaces. Formally, a persistence barcode consists of a multiset of intervals in the extended real line, where the length of each interval corresponds to the lifetime of a topological feature in a filtration, usually built on a point cloud, a graph, a function, or, more generally, a simplicial complex or a chain complex. Generally, longer intervals in a barcode correspond to more robust features, whereas shorter intervals are more likely to be noise in the data. A persistence barcode is a complete invariant that captures all the topological information in a filtration. In algebraic topology, the persistence barcodes were first introduced by Sergey Barannikov in 1994 as the "canonical forms" invariants consisting of a multiset of line segments with ends on two parallel lines, and later, in geometry processing, by Gunnar Carlsson et al. in 2004.

Definition

Let $\mathbb{𝔽}$ be a fixed field. Then a persistence module $M$ indexed over $\mathbb{ℝ}$ consists of a family of $\mathbb{𝔽}$-vector spaces $\{M_t{\}}_{t\in \mathbb{ℝ}}$ and linear maps ${\phi }_{s,t}:M_s\to M_t$ for each $s\le t$ such that ${\phi }_{s,t}\circ {\phi }_{r,s}={\phi }_{r,t}$ for all $r\le s\le t$. This construction is not specific to $\mathbb{ℝ}$; indeed, it works identically with any totally-ordered set.

A series of four nested simplicial complexes and the 0-dimensional persistence barcode of the resulting filtration.

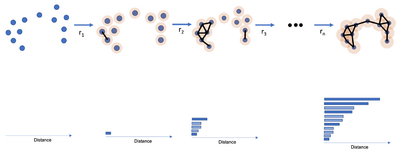
A persistence module $M$ is said to be of finite type if it contains a finite number of unique finite-dimensional vector spaces. The latter condition is sometimes referred to as pointwise finite-dimensional.

Let $I$ be an interval in $\mathbb{ℝ}$. Define a persistence module $Q(I)$ via $Q(I_s)=\{\begin{array}{ll}0,& \text{if }s\notin I;\\ \mathbb{𝔽},& \text{otherwise}\end{array}$, where the linear maps are the identity map inside the interval. The module $Q(I)$ is sometimes referred to as an interval module.

Then for any $\mathbb{ℝ}$-indexed persistence module $M$ of finite type, there exists a multiset ${{ℬ}}_M$ of intervals such that $M\cong \underset{I\in {{ℬ}}_M}{⨁}Q(I)$, where the direct sum of persistence modules is carried out index-wise. The multiset ${{ℬ}}_M$ is called the barcode of $M$, and it is unique up to a reordering of the intervals.

This result was extended to the case of pointwise finite-dimensional persistence modules indexed over an arbitrary totally-ordered set by William Crawley-Boevey and Magnus Botnan in 2020, building upon known results from the structure theorem for finitely generated modules over a PID, as well as the work of Cary Webb for the case of the integers.