Phase kickback

Short description: Mechanism in quantum computing

In quantum computing, phase kickback refers to the fact that controlled operations have effects on their controls, in addition to on their targets, and that these effects correspond to phasing operations. For example, when a controlled NOT gate's target qubit is in the state [math]\displaystyle{ 1/\sqrt{2} (|0\rangle - |1\rangle) }[/math], the effect of the controlled NOT gate is equivalent to the effect of applying a Pauli Z gate to the controlled NOT's control qubit. Phase kickback is one of the key effects that distinguishes quantum computation from classical computation. For example, phase kickback is the mechanism behind the Bernstein–Vazirani algorithm and more generally the quantum phase estimation algorithm. Phase kickback also provides a justification for why qubits would be disrupted by measurements: a measurement is an operation that flips a classical bit (the result) with the flip being controlled by a quantum bit (the qubit being measured). This creates kickback from the bit to the qubit, randomizing the qubit's phase.

Measuring an operator P (whose eigenvalues are +1 and -1) by using phase kickback onto the control of a controlled P operation.

A CNOT gate may appear to only act the control on the target, but surrounding it with Hadamard gates reveals it also acts the target on the control.

A CNOT appears asymmetric, but can be transformed into a symmetric operation by Hadamard gates. Symmetric operations don't distinguish target and control, resulting in effects like phase kickback.

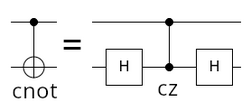
Phase kickback occurs because the basis transformations that distinguish targets from controls are available as operations. For example, surrounding a controlled NOT gate with four Hadamard gates produces a compound operation whose effect is equivalent to a controlled NOT gate, but with the roles of its control qubit and target qubit exchanged. More abstractly, phase kickback occurs because the eigendecomposition of controlled operations makes no significant distinction between controls and targets. For example, the controlled Z gate is a symmetric operation that has the same effect if its target and control are switched, and a controlled NOT gate can be decomposed into a Hadamard gate on its target, then a controlled Z gate, then a second Hadamard gate on its target. This decomposition reveals that, at the core of the apparently-asymmetric controlled-NOT gate, there is a symmetric effect that does not distinguish between control and target.

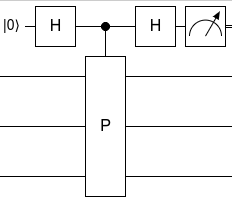
Phase kickback can be used to measure an operator [math]\displaystyle{ P }[/math] whose eigenvalues are +1 and -1. This is a common technique for measuring operators in quantum error correcting codes, such as the surface code. The procedure is as follows. Initialize a control qubit [math]\displaystyle{ c }[/math] in the [math]\displaystyle{ |0\rangle }[/math] state, then apply a Hadamard gate [math]\displaystyle{ H }[/math] to [math]\displaystyle{ c }[/math], then apply [math]\displaystyle{ P }[/math] controlled by [math]\displaystyle{ c }[/math], then apply another Hadamard gate [math]\displaystyle{ H }[/math] to [math]\displaystyle{ c }[/math], then measure [math]\displaystyle{ c }[/math] in the computational basis. Phase kickback results in the +1 eigenstates of [math]\displaystyle{ P }[/math] having no effect on [math]\displaystyle{ c }[/math], while -1 eigenstates apply a Pauli [math]\displaystyle{ Z }[/math] to [math]\displaystyle{ c }[/math]. The surrounding Hadamard gates turn the Pauli [math]\displaystyle{ Z }[/math] (a phase flip) into a Pauli [math]\displaystyle{ X }[/math] (a bit flip). So [math]\displaystyle{ c }[/math] gets flipped from [math]\displaystyle{ |0\rangle }[/math] to [math]\displaystyle{ |1\rangle }[/math] when the state is in the -1 eigenstate of [math]\displaystyle{ P }[/math]. The measurement operation reveals whether [math]\displaystyle{ c }[/math] is [math]\displaystyle{ |0\rangle }[/math] or [math]\displaystyle{ |1\rangle }[/math], which reveals whether the state was in the +1 or -1 eigenspace of [math]\displaystyle{ P }[/math].