Philosophy:Aristotle's axiom
Aristotle's axiom is an axiom in the foundations of geometry, proposed by Aristotle in On the Heavens that states:
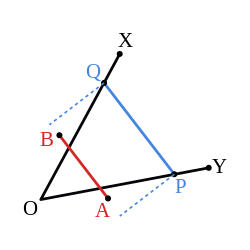
If [math]\displaystyle{ \widehat{\rm XOY} }[/math] is an acute angle and AB is any segment, then there exists a point P on the ray [math]\displaystyle{ \overrightarrow{OY} }[/math] and a point Q on the ray [math]\displaystyle{ \overrightarrow{OX} }[/math], such that PQ is perpendicular to OX and PQ > AB.
Aristotle's axiom is a consequence of the Archimedean property,[1] and the conjunction of Aristotle's axiom and the Lotschnittaxiom, which states that "Perpendiculars raised on each side of a right angle intersect", is equivalent to the Parallel Postulate.[2]
Without the parallel postulate, Aristotle's axiom is equivalent to each of the following three incidence-geometric statements:[3]
- Given a line A and a point P on A, as well as two intersecting lines M and N, both parallel to A there exists a line G through P which intersects M but not N.
- Given a line A as well as two intersecting lines M and N, both parallel to A, there exists a line G which intersects A and M, but not N.
- Given a line A and two distinct intersecting lines M and N, each different from A, there exists a line G which intersects A and M, but not N.
References
- ↑ Pambuccian, Victor (2019), "The elementary Archimedean axiom in absolute geometry (Paper No. 52)", Journal of Geometry 110: 1–9, doi:10.1007/s00022-019-0507-x, https://link.springer.com/article/10.1007/s00022-019-0507-x
- ↑ Pambuccian, Victor (1994), "Zum Stufenaufbau des Parallelenaxioms", Journal of Geometry 51 (1–2): 79–88, doi:10.1007/BF01226859, https://link.springer.com/article/10.1007%2FBF01226859
- ↑ Pambuccian, Victor; Schacht, Celia (2021), "The ubiquitous axiom", Results in Mathematics 76 (3): 1–39, doi:10.1007/s00025-021-01424-3, https://link.springer.com/article/10.1007/s00025-021-01424-3
Sources
- Greenberg, Marvin Jay (1988), "Aristotle's axiom in the foundations of geometry", Journal of Geometry 33 (1–2): 53–57, doi:10.1007/BF01230603, https://link.springer.com/article/10.1007/BF01230603
- Greenberg, Marvin Jay (2010), "Old and new results in the foundations of elementary plane Euclidean and non-Euclidean geometries", American Mathematical Monthly 117 (3): 198–219, doi:10.4169/000298910x480063, https://www.maa.org/sites/default/files/pdf/upload_library/22/Ford/Greenberg2011.pdf
- Greenberg, Marvin Jay (2008), Euclidean and non-Euclidean geometries, 4th edition, W H Freeman
- Martin, George E. (1982), The foundations of geometry and the non-Euclidean plane, Springer
- Pambuccian, Victor (2019), "The elementary Archimedean axiom in absolute geometry (Paper No. 52)", Journal of Geometry 110: 1–9, doi:10.1007/s00022-019-0507-x, https://link.springer.com/article/10.1007/s00022-019-0507-x
- Pambuccian, Victor (1994), "Zum Stufenaufbau des Parallelenaxioms", Journal of Geometry 51 (1–2): 79–88, doi:10.1007/BF01226859, https://link.springer.com/article/10.1007%2FBF01226859
- Pambuccian, Victor; Schacht, Celia (2021), "The ubiquitous axiom", Results in Mathematics 76 (3): 1–39, doi:10.1007/s00025-021-01424-3, https://link.springer.com/article/10.1007/s00025-021-01424-3
 |