Physics:Anchor Force Equation (proof)

The load is pointing straight down, and is being held up by two forces pointing up at various angles $\alpha$ and $\beta$.

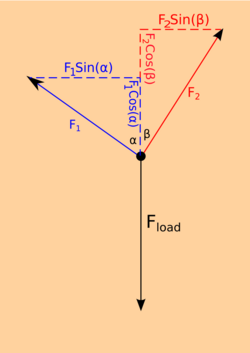
Equalization is a mathematical analysis of static load-sharing (also called load-distributing) 2-point anchor systems. To clarify, equalization is the method to find tension on two cables sharing a single load, but with different lengths, and angles to the load.

Derivation

Consider the node, where the two anchor legs join with the main line. At this node, the sum of all forces in the x-direction must equal zero since the system is in mechanical equilibrium.

$F_{x1}=F_{x2}$

$F_1\sin (\alpha )=F_2\sin (\beta )$

$F_1=F_2\frac{\sin (\beta )}{\sin (\alpha )}$

(1)

The net force in the y-direction must also sum to zero.

$F_{y1}+F_{y2}=F_{load}$

$F_1\cos (\alpha )+F_2\cos (\beta )=F_{load}$

(2)

Substitute $F_1$ from equation (1) into equation (2) and factor out $F_2$.

$F_2\frac{\sin (\beta )}{\sin (\alpha )}\cos (\alpha )+F_2\cos (\beta )=F_{load}$

$F_2[\frac{\sin (\beta )}{\sin (\alpha )}\cos (\alpha )+\cos (\beta )]=F_{load}$

Solve for $F_2$ and simplify.

$F_2=\frac{F_{load}}{[\frac{\sin (\beta )}{\sin (\alpha )}\cos (\alpha )+\cos (\beta )]}$

$F_2=\frac{F_{load}}{[\frac{\sin (\beta )\cos (\alpha )}{\sin (\alpha )}+\frac{\cos (\beta )\sin (\alpha )}{\sin (\alpha )}]}$

$F_2=\frac{F_{load}}{\left[\frac{\cos (\alpha )\sin (\beta )+\sin (\alpha )\cos (\beta )}{\sin (\alpha )}\right]}$

$F_2=F_{load}\frac{\sin (\alpha )}{\cos (\alpha )\sin (\beta )+\sin (\alpha )\cos (\beta )}$

Use a trigonometric identity to simplify more and arrive at our final solution for $F_2$.

$F_2=F_{load}\frac{\sin (\alpha )}{\sin (\alpha +\beta )}$

(3)

Then use $F_2$ from equation (3) and substitute into (1) to solve for $F_1$

$F_1=F_{load}\frac{\sin (\alpha )}{\sin (\alpha +\beta )}\frac{\sin (\beta )}{\sin (\alpha )}$

$F_1=F_{load}\frac{\sin (\beta )}{\sin (\alpha +\beta )}$

(4)

Symmetrical Anchor - Special Case

This diagram shows the specific case when the anchor is symmetrical. Notice $2\alpha =\theta$.

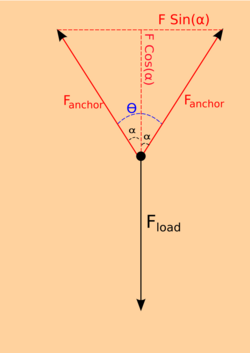
Let us now analyze a specific case in which the two anchors are "symmetrical" along the y-axis.

Start by noticing $\alpha$ and $\beta$ are the same. Let us start from equation (4) and substitute $\beta$ for $\alpha$ and simplify.

$F_{eachAnchor}=F_{load}\frac{Sin(\alpha )}{Sin(\alpha +\alpha )}$

$F_{eachAnchor}=F_{load}\frac{Sin(\alpha )}{Sin(2\alpha )}$

And using another trigonometric identity we can simplify the denominator.

$F_{eachAnchor}=F_{load}\frac{Sin(\alpha )}{2Sin(\alpha )Cos(\alpha )}$

$F_{eachAnchor}=\frac{F_{load}}{2Cos(\alpha )}$

Note that $\alpha$ is half of the angle $\theta$ between the two anchor points. To express the force at each anchor using the entire angle $\theta$, we substitute $\alpha =\theta /2$.

$F_{eachAnchor}=\frac{F_{load}}{2Cos(\frac{\theta }{2})}$

References

• "Non-Load Sharing Anchors." Ratref. Web. 11 February 2012. <https://web.archive.org/web/20100613015052/http://ratref.com/content/non-load-sharing-anchors>.