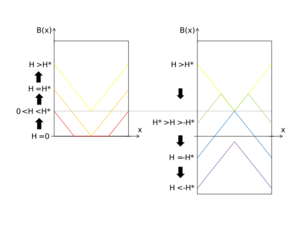Physics:Bean's critical state model

Short description: Theoretical model for magnetic behaviour of some superconductors

Calculated magnetization curve for a superconducting slab, based on Bean's model. The superconducting slab is initially at H = 0. Increasing H to critical field H* causes the blue curve; dropping H back to 0 and reversing direction to increase it to -H* causes the green curve; dropping H back to 0 again and increase H to H* causes the orange curve.

Bean's critical state model, introduced by C. P. Bean in 1962, gives a macroscopic explanation of the irreversible magnetization behavior (hysteresis) of hard Type-II superconductors.

Assumptions

Hard superconductors often exhibit hysteresis in magnetization measurements. C. P. Bean postulated for the Shubnikov phase an extraordinary shielding process due to the microscopic structure of the materials. He assumed lossless transport with a critical current density J_c(B) (J_c(B→0) = const. and J_c(B→∞) = 0). An external magnetic field is shielded in the Meissner phase (H < H_c1) in the same way than in a soft superconductor. In the Shubnikov phase (H_c1 < H < H_c2), the critical current flows below the surface within a depth necessary to reduce the field in the inside of the superconductor to H_c1.

Explanation of the irreversible magnetization

A schematic of the magnetic field distribution in a superconducting cylinder during the change of external magnetic field H, based on Bean's model.

To understand the origin of the irreversible magnetization: assume a hollow cylinder in an external magnetic field parallel to the cylinder axis. In the Meissner phase, a screening current is within the London penetration depth. Exceeding H_c1, vortices start to penetrate into the superconductor. These vortices are pinned on the surface (Bean–Livingston barrier). In the area below the surface, which is penetrated by the vortices, is a current with the density J_c. At low fields (H < H₀), the vortices do not reach the inner surface of the hollow cylinder and the interior stays field-free. For H > H₀, the vortices penetrate the whole cylinder and a magnetic field appears in the interior, which then increases with increasing external field. Let us now consider what happens, if the external field is then decreased: Due to induction, an opposed critical current is generated at the outer surface of the cylinder keeping inside the magnetic field for H₀ < H < H₁ constant. For H > H₁, the opposed critical current penetrates the whole cylinder and the inner magnetic field starts to decrease with decreasing external field. When the external field vanishes, a remnant internal magnetic field occurs (comparable to the remanent magnetization of a ferromagnet). With an opposed external field H₀, the internal magnetic field finally reaches 0T (H₀ equates the coercive field of a ferromagnet).

Extensions

Bean assumed a constant critical current meaning that H << H_c2. Kim et al. extended the model assuming 1/J(H) proportional to H, yielding excellent agreement of theory and measurements on Nb₃Sn tubes. Different geometries have to be considered as the irreversible magnetization depends on the sample geometry.