Physics:Channel sounding

Short description: Wireless signal analysis technique

Channel sounding is a technique that evaluates a radio environment for wireless communication, especially MIMO systems. Because of the effect of terrain and obstacles, wireless signals propagate in multiple paths (the multipath effect). To minimize or use the multipath effect, engineers use channel sounding to process the multidimensional spatial–temporal signal and estimate channel characteristics. This helps simulate and design wireless systems.

Motivation & applications

Mobile radio communication performance is significantly affected by the radio propagation environment. Blocking by buildings and natural obstacles creates multiple paths between the transmitter and the receiver, with different time variances, phases and attenuations. In a single-input, single-output (SISO) system, multiple propagation paths can create problems for signal optimization. However, based on the development of multiple input, multiple output (MIMO) systems, it can enhance channel capacity and improve QoS. In order to evaluate effectiveness of these multiple antenna systems, a measurement of the radio environment is needed. Channel sounding is such a technique that can estimate the channel characteristics for the simulation and design of antenna arrays.

Problem statement & basics

MIMO sounding

In a multipath system, the wireless channel is frequency dependent, time dependent, and position dependent. Therefore, the following parameters describe the channel:

• Direction of departure (DOD)
• Direction of arrival (DOA)
• Time delay
• Doppler shift
• Complex polarimetric path weight matrix

To characterize the propagation path between each transmitter element and each receiver element, engineers transmit a broadband multi-tone test signal. The transmitter's continuous periodic test sequence arrives at the receiver, and is correlated with the original sequence. This impulse-like auto correlation function is called channel impulse response (CIR). By obtaining the transfer function of CIR, we can make an estimation of the channel environment and improve the performance.

Description of existing approaches

MIMO Vector Channel Sounder

Based on multiple antennas at both transmitters and receivers, a MIMO vector channel sounder can effectively collect the propagation direction at both ends of the connection and significantly improve resolution of the multiple path parameters.

K-D model of wave propagation

Planar wave model

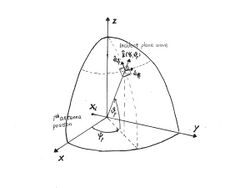
Engineers model wave propagation as a finite sum of discrete, locally planar waves instead of a ray tracing model. This reduces computation and lowers requirements for optics knowledge. The waves are considered planar between the transmitters and the receivers. Two other important assumptions are:

• Relative bandwidth is small enough so that the time delay can be simply transformed to a phase shift among the antennas.
• The array aperture is small enough that there is no observable magnitude variation.

Based on such assumptions, the basic signal model is described as:

[math]\displaystyle{ h(\alpha,\tau,\psi_R,\upsilon_R,\psi_T,\upsilon_T) = \sum_{p=1}^P \gamma_p\delta(\alpha-\alpha_p)\delta(\tau-\tau_p)\cdot\delta(\psi_R-\psi_{R_p})\delta(\upsilon_R-\upsilon_{R_p})\cdot\delta(\psi_T-\psi_{T_p})\delta(\upsilon_T-\upsilon_{T_p}) }[/math]

where [math]\displaystyle{ \tau_p }[/math] is the TDOA (Time Difference of Arrival) of the wave-front [math]\displaystyle{ p }[/math]. [math]\displaystyle{ \psi_{R_p},\upsilon_{R_p} }[/math] are DOA at the receiver and [math]\displaystyle{ \psi_{T_p},\upsilon_{T_p} }[/math] are DOD at the transmitter,[math]\displaystyle{ \alpha_p }[/math] is the Doppler shift.

Real-Time Ultra-wideband MIMO Channel Sounding

A higher bandwidth for channel measurement is a goal for future sounding devices. The new real-time UWB channel sounder can measure the channel in a larger bandwidth from near zero to 5 GHz. The real time UWB MIMO channel sounding is greatly improving accuracy of localization and detection, which facilitates precisely tracking mobile devices.

Excitation signal

A multitoned signal is chosen as the excitation signal.

[math]\displaystyle{ x(t) = \sum_{k=-N_c/2}^{N_c/2-1} \sin(2\pi(f_c+k\cdot\Delta f)\cdot t+\theta_k) }[/math]

where [math]\displaystyle{ f_c }[/math] is the center frequency, [math]\displaystyle{ \Delta f = B/N_c }[/math] ([math]\displaystyle{ B }[/math] is Bandwidth, [math]\displaystyle{ N_c }[/math] is Number of multitones) is the tone spacing, and [math]\displaystyle{ \theta_k }[/math] is the phase of the [math]\displaystyle{ k^{th} }[/math] tone. we can obtain [math]\displaystyle{ \theta_k }[/math] by

[math]\displaystyle{ \theta_k = {{(\pi\cdot k)}^2 \over N_c / 2} }[/math]

Data post-processing

RUSK SOUNDING. [math]\displaystyle{ \alpha_{max} }[/math] is the maximum Doppler frequency.[math]\displaystyle{ \tau_{max} }[/math] is the maximum duration of the impulse response and S is the channel's spread (the red rectangle in the figure).

1. A DFT over K-1 (one waveform lost due to array switching) waveforms that measured in each channel is performed (K: waveforms per channel).
2. The frequency domain samples at the multitone frequencies are picked at every [math]\displaystyle{ (K-1)^{th} }[/math] sample.
3. An estimated channel transfer function [math]\displaystyle{ \hat{H}(f) }[/math] is obtained by:

[math]\displaystyle{ \hat{H}(f) = {X_{ref}(f)^*\cdot Y(f) \over {\left|X_{ref}(f)\right|}^2+c\cdot\hat{\sigma}_N^2(f)} }[/math]

where [math]\displaystyle{ \hat{\sigma}_N^2(f) }[/math] is the noise power, [math]\displaystyle{ X_{ref}(f) }[/math] is a reference signal and [math]\displaystyle{ Y(f) }[/math] is the samples. The scaling factor c is defined as

[math]\displaystyle{ c = {\bar{\sigma}_{ref}^2 \over max{(\bar{\sigma}_{Y}^2}-\bar{\sigma}_{N}^2),\bar{\sigma}_{N}^2} }[/math]

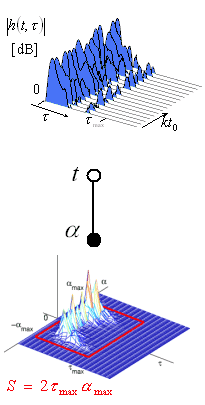
RUSK Channel Sounder

A RUSK channel sounder excites all frequencies simultaneously, so that the frequency response of all frequencies can be measured. The test signal is periodic in time with period [math]\displaystyle{ t_p }[/math]. The period must be longer than the duration of the channel's impulse response [math]\displaystyle{ \tau_{max} }[/math] in order to capture all delayed multipath components at the receiver. The figure shows a typical channel impulse response (CIR) for a RUSK sounder. A secondary time variable is introduced so that the CIR is a function of the delay time [math]\displaystyle{ \tau }[/math] and the observation time [math]\displaystyle{ t }[/math]. A delay-Doppler spectrum is obtained by Fourier transformation.

See also

• Channel estimation