Physics:Charge-transfer insulators

A comparison between charge-transfer and Mott-Hubbard insulator band structures: a cuprate vs a nickelate.

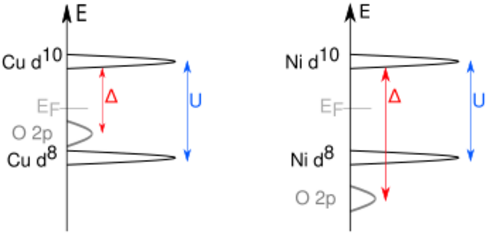
Charge-transfer insulators are a class of materials predicted to be conductors following conventional band theory, but which are in fact insulators due to a charge-transfer process. Unlike in Mott insulators, where the insulating properties arise from electrons hopping between unit cells, the electrons in charge-transfer insulators move between atoms within the unit cell. In the Mott–Hubbard case, it's easier for electrons to transfer between two adjacent metal sites (on-site Coulomb interaction U); here we have an excitation corresponding to the Coulomb energy U with

$d^n{d}^n\to d^{n-1}{d}^{n+1},\mathrm{\Delta }E=U=U_{dd}$.

In the charge-transfer case, the excitation happens from the anion (e.g., oxygen) p level to the metal d level with the charge-transfer energy Δ:

$d^n{p}^6\to d^{n+1}{p}^5,\mathrm{\Delta }E={\mathrm{\Delta }}_{CT}$.

U is determined by repulsive/exchange effects between the cation valence electrons. Δ is tuned by the chemistry between the cation and anion. One important difference is the creation of an oxygen p hole, corresponding to the change from a 'normal' $\mathrm{O}{\phantom{A}}^{2-}$ to the ionic $\mathrm{O}{\phantom{A}}^{-}$ state. In this case the ligand hole is often denoted as $\underset{\_}{L}$.

Distinguishing between Mott-Hubbard and charge-transfer insulators can be done using the Zaanen-Sawatzky-Allen (ZSA) scheme.

Exchange interaction

Analogous to Mott insulators we also have to consider superexchange in charge-transfer insulators. One contribution is similar to the Mott case: the hopping of a d electron from one transition metal site to another and then back the same way. This process can be written as

$d_i^n{p}^6{d}_j^n\to d_i^n{p}^5{d}_j^{n+1}\to d_i^{n-1}{p}^6{d}_j^{n+1}\to d_i^n{p}^5{d}_j^{n+1}\to d_i^n{p}^6{d}_j^n$.

This will result in an antiferromagnetic exchange (for nondegenerate d levels) with an exchange constant $J=J_{dd}$.

$J_{dd}=\frac{2t_{dd}^2}{U_{dd}}=\frac{2t_{pd}^4}{{\mathrm{\Delta }}_{CT}^2{U}_{dd}}$

In the charge-transfer insulator case

$d_i^n{p}^6{d}_j^n\to d_i^n{p}^5{d}_j^{n+1}\to d_i^{n+1}{p}^4{d}_j^{n+1}\to d_i^{n+1}{p}^5{d}_j^n\to d_i^n{p}^6{d}_j^n$.

This process also yields an antiferromagnetic exchange $J_{pd}$:

$J_{pd}=\frac{4t_{pd}^4}{{\mathrm{\Delta }}_{CT}^2\cdot (2{\mathrm{\Delta }}_{CT}+U_{pp})}$

The difference between these two possibilities is the intermediate state, which has one ligand hole for the first exchange ($p^6\to p^5$) and two for the second ($p^6\to p^4$).

The total exchange energy is the sum of both contributions:

$J_{total}=\frac{2t_{pd}^4}{{\mathrm{\Delta }}_{CT}^2}\cdot (\frac{1}{U_{dd}}+\frac{1}{{\mathrm{\Delta }}_{CT}+\frac{1}{2}{U}_{pp}})$.

Depending on the ratio of $U_{dd}\text{ and }({\mathrm{\Delta }}_{CT}+\frac{1}{2}{U}_{pp})$, the process is dominated by one of the terms and thus the resulting state is either Mott-Hubbard or charge-transfer insulating.