Physics:Cophonicity
Given two interacting atoms A and B, the cophonicity (/koʊfoʊˈnɪsɪti/) of the A-B atomic pair is a measure of the overlap of the A and B contributions to a specific range of vibrational frequencies. In the field of condensed matter physics, cophonicity is a metric aimed at the parametrization of the dynamical interactions in terms of the atomic types forming the A-B pair. In connection with other electronic and structural descriptors, such as the covalency metric[1] or the distortion mode analysis[2] from group theory, the A-B pair cophonicity is a guide to properly select either A or B atomic species to tune specific vibrational frequencies of a given system. The cophonicity metric has been originally designed[3][4][5] for the study of the atomic motions in transition metal dichalcogenides, but its formulation is general and can be applied to any kind of system, irrespective of the chemical composition and stoichiometry.[6][7][8][9][10]
Mathematical formulation
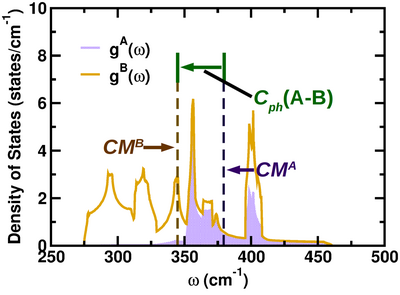
Considering the phonon density of states (pDOS) in the first Brillouin zone, the center mass of the atom-projected pDOS of an atom A is defined as
where is the contribution of the atom A to and ; the total density of states of the solid is , defined as
and obtained by summing over all atoms X of the unit cell. The integration interval is chosen in such a way that it encompasses all the phonon states relevant for the specific study. The integral at the denominator of the definition of is the contribution of the atom A to the states in the frequency range ; we call such quantity the phonicity of the A atom in that specific frequency range. The phonicity of an atom then represents the amount of phonon states that such atom contributes to form; in this respect, it can be regarded as the phonon counterpart of the atomic valence, that is the number of electrons with which an atom participates to form the electronic states of the system, counted as the integral of the atom-projected electronic density of states.
Consider a generic A-B atomic pair. The relative position of the center mass of with respect to the center mass of is given as
which is specified in the same units of the frequency . A positive (negative) sign of indicates that the A (B) atom contributes more to the high frequency modes of the specified range. The smaller is , the higher is the mixing of the A and B contributions to the frequency band, and the two atoms have the same weight in the determination of the modes specific of the considered energy range. We define the quantity as the cophonicity of the A-B atomic pair, in analogy with the A-B bond covalency definition formulated in terms of atomic contributions to the electronic density of states.[1]
Cophonicity is then a characteristic of a specific atomic pair found in a system. According to the metric introduced above, would indicate a perfect cophonocity, that is an equal participation of both atomic species to the formation of the phonon states in the considered range of energies.
The comparison between two cophonicity values, obtained considering distinct atomic couples embedded in two structures with different connectivity, will provide meaningful information under certain conditions. For example, in molybdenum disulfide bulk and nanoclusters, despite calculated in the same frequency range, could refer to distinct sets of vibrational modes; this is due to the distinct topologies that, in turn, determine different electronic environments. In this case, any change of the cophonicity by means of substitutional defects could lead to non-correlated changes of the vibrational frequencies. However, if the two structures with distinct topologies are connected by continuous geometric transformations, also the electronic environment of the atomic pairs, thus the vibrational frequencies and the associated modes, are related by such continuous transformations; in this case, the cophonicity of a specific atomic pair in one structure can be mapped into the cophonicity of the second one, granting the transferability of the definition, hence the reliability of the cophonicity comparison.
References
- ↑ 1.0 1.1 Cammarata, Antonio; Rondinelli, James M. (21 September 2014). "Covalent dependence of octahedral rotations in orthorhombic perovskite oxides". The Journal of Chemical Physics 141 (11): 114704. doi:10.1063/1.4895967. PMID 25240365. Bibcode: 2014JChPh.141k4704C.
- ↑ Campbell, J.; Stokes, H.; Tanner, D.; Hatch, D. (2006). "ISODISPLACE: a web-based tool for exploring structural distortions". Journal of Applied Crystallography 39 (4): 214804. doi:10.1107/S0021889806014075.
- ↑ Cammarata, Antonio; Polcar, Tomas (2015). "Tailoring Nanoscale Friction in MX2 Transition Metal Dichalcogenides". Inorg. Chem. 54 (12): 5739–5744. doi:10.1021/acs.inorgchem.5b00431. PMID 26000720.
- ↑ Cammarata, Antonio; Polcar, Tomas (2015). "Electro-vibrational Coupling Effects on "Intrinsic Friction" in Transition Metal Dichalcogenides". RSC Adv. 5 (129): 106809–106818. doi:10.1039/c5ra24837j. Bibcode: 2015RSCAd...5j6809C.
- ↑ Cammarata, Antonio; Polcar, Tomas (2016). "Layering Effects on Low Frequency Modes in n-layered MX2 Transition Metal Dichalcogenides". Phys. Chem. Chem. Phys. 18 (6): 4807–4813. doi:10.1039/c5cp06788j. PMID 26806673. Bibcode: 2016PCCP...18.4807C.
- ↑ Hu, Tao; Hu, Minmin; Li, Zhaojin; Zhang, Hui; Zhang, Chao; Wang, Jiemin; Wang, Xiaohui (31 December 2015). "Covalency-Dependent Vibrational Dynamics in Two-Dimensional Titanium Carbides". The Journal of Physical Chemistry A 119 (52): 12977–12984. doi:10.1021/acs.jpca.5b08626. PMID 26652906. Bibcode: 2015JPCA..11912977H.
- ↑ Banerjee, Tushar; Chattopadhyay, A. K. (2015-11-25). "Structural, mechanical and tribological properties of pulsed DC magnetron sputtered TiN–WSx/TiN bilayer coating". Surface and Coatings Technology 282: 24–35. doi:10.1016/j.surfcoat.2015.10.011.
- ↑ Lu, Ziheng; Chen, Chi; Baiyee, Zarah Medina; Chen, Xin; Niu, Chunming; Ciucci, Francesco (2015). "Defect chemistry and lithium transport in Li 3 OCl anti-perovskite superionic conductors" (in en). Phys. Chem. Chem. Phys. 17 (48): 32547–32555. doi:10.1039/c5cp05722a. PMID 26597695. Bibcode: 2015PCCP...1732547L.
- ↑ Tedstone, Aleksander A.; Lewis, David J.; O'Brien, Paul (2016-04-12). "Synthesis, Properties, and Applications of Transition Metal-Doped Layered Transition Metal Dichalcogenides". Chemistry of Materials 28 (7): 1965–1974. doi:10.1021/acs.chemmater.6b00430. ISSN 0897-4756.
- ↑ Fei, Ruixiang; Kang, Wei; Yang, Li (2016-08-23). "Ferroelectricity and Phase Transitions in Monolayer Group-IV Monochalcogenides". Physical Review Letters 117 (9). doi:10.1103/PhysRevLett.117.097601. PMID 27610884. Bibcode: 2016PhRvL.117i7601F. https://zenodo.org/record/1064201.
 |
