Physics:Diffusion (acoustics)

Diffusion, in architectural acoustics, is the spreading of sound energy evenly in a given environment. A perfectly diffusive sound space is one in which the reverberation time is the same at any listening position. Most interior spaces are non-diffusive; the reverberation time is considerably different around the room. At low frequencies, they suffer from prominent resonances called room modes.
Diffusor
Diffusors (or diffusers) are used to treat sound aberrations, such as echoes, in rooms. They are an excellent alternative or complement to sound absorption because they do not remove sound energy, but can be used to effectively reduce distinct echoes and reflections while still leaving a live sounding space. Compared to a reflective surface, which will cause most of the energy to be reflected off at an angle equal to the angle of incidence, a diffusor will cause the sound energy to be radiated in many directions, hence leading to a more diffusive acoustic space. It is also important that a diffusor spreads reflections in time as well as spatially. Diffusors can aid sound diffusion, but this is not why they are used in many cases; they are more often used to remove coloration and echoes.
Diffusors come in many shapes and materials. The birth of modern diffusors was marked by Manfred R. Schroeders' invention of number-theoretic diffusors in the 1970s. He got the idea during a 1977 Göttingen lecture by André Weil, Gauss sums and quadratic residues, celebrating the 200th anniversary of the birth of Gauss.[1]
Maximum length sequence diffusors

Maximum length sequence based diffusors are made of strips of material with two different depths. The placement of these strips follows an MLS. The width of the strips is smaller than or equal to quarter the wavelength of the frequency where the maximum scattering effect is desired. Ideally, small vertical walls are placed between lower strips, improving the scattering effect in the case of tangential sound incidence. The bandwidth of these devices is rather limited; at one octave above the design frequency, diffusor efficiency drops to that of a flat surface.
Quadratic-residue diffusors

MLS based diffusors are superior to geometrical diffusors in many respects; they have limited bandwidth. The new goal was to find a new surface geometry that would combine the excellent diffusion characteristics of MLS designs with wider bandwidth. A new design was discovered, called a quadratic residue diffusor.[2] Today the quadratic residue diffusor or Schroeder diffusor is still widely used. Quadratic-Residue Diffusors can be designed to diffuse sound in either one or two directions.
Primitive-root diffusors
Primitive-root diffusors are based on a number theoretic sequence based on primitive roots. Although they produce a notch in the scattering response, in reality the notch is over too narrow a bandwidth to be useful. In terms of performance, they are very similar to Quadratic-Residue Diffusors.[3][4]
Optimized diffusors
By using numerical optimisation, it is possible to increase the number of theoretical designs, especially for diffusors with a small number of wells per period. But the big advantage of optimisation is that arbitrary shapes can be used which can blend better with architectural forms.
Two-dimensional ("hemispherical") diffusors
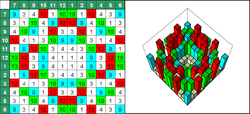
Designed, like most diffusors, to create "a big sound in a small room," unlike other diffusors, two-dimensional diffusors scatter sound in a hemispherical pattern. This is done by the creation of a grid, whose cavities have wells of varying depth, according to the matrix addition of two quadratic sequences equal or proportionate to those of a regular diffusor.[5] These diffusors are very helpful for controlling the direction of the diffusion, particularly in studios and control rooms.[6]
See also
References
- ↑ Xiang, Ning, ed (2015). "20: Bell Laboratories" (in en). Acoustics, Information, and Communication: Memorial Volume in Honor of Manfred R. Schroeder. Cham: Springer International Publishing. pp. 396. doi:10.1007/978-3-319-05660-9. ISBN 978-3-319-05659-3. https://link.springer.com/10.1007/978-3-319-05660-9.
- ↑ M. R. Schroeder (April 1979). "Binaural dissimilarity and optimum ceilings for concert halls: More lateral sound diffusion". J. Acoust. Soc. Am. 65 (4): 958–963. doi:10.1121/1.382601. Bibcode: 1979ASAJ...65..958S.
- ↑ Eliot Feldman (July 1995). "A reflection grating that nullifies the specular reflection: A cone of silence". The Journal of the Acoustical Society of America 98 (1): 623–634. doi:10.1121/1.413656. Bibcode: 1995ASAJ...98..623F.
- ↑ Walker, R. "The design and application of modular acoustic diffusing elements". BBC Research Department. http://downloads.bbc.co.uk/rd/pubs/reports/1990-15.pdf. Retrieved 25 March 2019.
- ↑ Strube, Hans Werner (1981). "More on the diffraction theory of Schroeder diffusors". The Journal of the Acoustical Society of America (Acoustical Society of America (ASA)) 70 (2): 633–635. doi:10.1121/1.386757. ISSN 0001-4966.
- ↑ "The effects of 2d diffusers on sound diffusion". PF. http://www.partfoam.com/qrdacousticpanel.html. (in Dari)
Further reading
- T. J. Cox and P. D'Antonio, Acoustic Absorbers and Diffusors - Theory, Design and Application Spon press.
- M. R. Schroeder, Number Theory in Science and Communication, Springer-Verlag, 1984; see especially sections 15.8 and 26.6.
 |
