Physics:Diffusive–thermal instability
Diffusive–thermal instability or thermo–diffusive instability is an intrinsic flame instability that occurs both in premixed flames and in diffusion flames and arises because of the difference in the diffusion coefficient values for the fuel and heat transport, characterized by non-unity values of Lewis numbers. The instability mechanism that arises here is the same as in Turing instability explaining chemical morphogenesis, although the mechanism was first discovered in the context of combustion by Yakov Zeldovich in 1944 to explain the cellular structures appearing in lean hydrogen flames.[1] Quantitative stability theory for premixed flames were developed by Gregory Sivashinsky (1977),[2] Guy Joulin and Paul Clavin (1979)[3] and for diffusion flames by Jong S. Kim and Forman A. Williams (1996,1997).[4][5][6]
Dispersion relation for premixed flames
To neglect the influences by hydrodynamic instabilities such as Darrieus–Landau instability, Rayleigh–Taylor instability etc., the analysis usually neglects effects due to the thermal expansion of the gas mixture by assuming a constant density model. Such an approximation is referred to as diffusive-thermal approximation or thermo-diffusive approximation which was first introudced by Grigory Barenblatt, Yakov Zeldovich and A. G. Istratov in 1962.[7] With a one-step chemistry model and assuming the perturbations to a steady planar flame in the form [math]\displaystyle{ e^{i\mathbf{k}\cdot\mathbf{x}_\bot+\omega t} }[/math], where [math]\displaystyle{ \mathbf{x}_\bot }[/math] is the transverse coordinate system perpendicular to flame, [math]\displaystyle{ t }[/math] is the time, [math]\displaystyle{ \mathbf{k} }[/math] is the perturbation wavevector and [math]\displaystyle{ \omega }[/math] is the temporal growth rate of the disturbance, the dispersion relation [math]\displaystyle{ \omega(k) }[/math] for one-reactant flames is given implicitly by[8][9]
- [math]\displaystyle{ 2\Gamma^2(\Gamma-1) + l (\Gamma-1 - 2 \omega) = 0 }[/math]
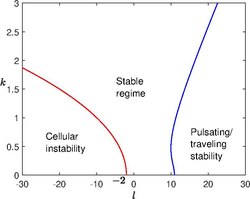
where [math]\displaystyle{ \Gamma=\sqrt{1+4\omega+4k^2} }[/math], [math]\displaystyle{ l\equiv (Le-1)/\beta }[/math], [math]\displaystyle{ Le }[/math] is the Lewis number of the fuel and [math]\displaystyle{ \beta }[/math] is the Zeldovich number. This relation provides in general three roots for [math]\displaystyle{ \omega }[/math] in which the one with maximum [math]\displaystyle{ \Re\{\omega\} }[/math] would determine the stability character. The stability margins are given by the following equations
- [math]\displaystyle{ 8k^2 + l + 2 =0, \quad 256 k^4 +(-6l^2+32l+256)k^2 -l^2+8l + 32=0 }[/math]
describing two curves in the [math]\displaystyle{ l }[/math]vs.[math]\displaystyle{ k }[/math] plane. The first curve is associated with condition [math]\displaystyle{ \Im\{\omega\}=0 }[/math], whereas on the second curve [math]\displaystyle{ \Im\{\omega\}\neq 0. }[/math] The first curve separates the region of stable mode from the region corresponding to cellular instability, whereas the second condition indicates the presence of traveling and/or pulsating instability.
See also
- Turing pattern
- Darrieus–Landau instability
- Kuramoto–Sivashinsky equation
- Double diffusive convection
References
- ↑ (1944). Theory of Combustion and Detonation of Gases. In R. Sunyaev (Ed.), Selected Works of Yakov Borisovich Zeldovich, Volume I: Chemical Physics and Hydrodynanics (pp. 162-232). Princeton: Princeton University Press.
- ↑ Sivashinsky, G. I. (1977). Diffusional-thermal theory of cellular flames. Combustion Science and Technology, 15(3-4), 137-145.
- ↑ Joulin, G., & Clavin, P. (1979). Linear stability analysis of nonadiabatic flames: diffusional-thermal model. Combustion and Flame, 35, 139-153.
- ↑ Kim, J. S. (1997). Linear analysis of diffusional-thermal instability in diffusion flames with Lewis numbers close to unity. Combustion Theory and Modelling, 1(1), 13.
- ↑ Kim, J. S., Williams, F. A., & Ronney, P. D. (1996). Diffusional-thermal instability of diffusion flames. Journal of Fluid mechanics, 327, 273-301.
- ↑ Kim, J. S., & Lee, S. R. (1999). Diffusional-thermal instability in strained diffusion flames with unequal Lewis numbers. Combustion Theory and Modelling, 3(1), 123.
- ↑ Barenblatt, G. I., Zeldovich Ya. B., Istratov, A. G. (1962). On diffusional-thermal stability of a laminar flame. J. Appl. Mech. Tech. Phys., 4, 21-26.
- ↑ Williams, F. A. (2018). Combustion theory. CRC Press.
- ↑ Clavin, P., & Searby, G. (2016). Combustion waves and fronts in flows: flames, shocks, detonations, ablation fronts and explosion of stars. Cambridge University Press.
 |  |
