Physics:Dislocation avalanches

From HandWiki

Dislocation avalanches are rapid discrete events during plastic deformation, in which defects are reorganized collectively. This intermittent flow behavior has been observed in microcrystals, whereas macroscopic plasticity appears as a smooth process. Intermittent plastic flow has been observed in several different systems. In AlMg Alloys, interaction between solute and dislocations can cause sudden jump during dynamic strain aging.[1] In metallic glass, it can be observed via shear banding with stress localization;[2] and single crystal plasticity, it shows up as slip burst.[3] However, analysis of the events with orders-magnitude difference in sizes with different crystallographic structure reveals power-law scaling between the number of events and their magnitude, or scale-free flow.[4] This microscopic instability of plasticity can have profound consequences on mechanical behavior of microcrystals. The increased relative size of the fluctuations makes it difficult to control the plastic forming process.[5] Moreover, at small specimen sizes the yield stress is not well defined by the 0.2% plastic strain criterion anymore, since this value varies specimen by specimen.[6]

Similar intermittent effects has been studied in many completely different systems, including intermittency of energy dissipation in magnetism (Barkhausen effect), superconductivity, earthquakes, and friction.[7]

Background

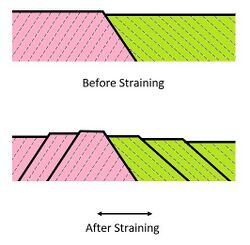
Slip bands formation near a grain boundary. The dashed lines stand for slip planes

Macroscopic plasticity are well-described by continuum model. Dislocations motions are characterized by an average velocity

[math]\displaystyle{ \tau = \rho b \bar{v} }[/math]

which is known as Orowan's equation. However, this approach completely fails to account for well-known intermittent deformation phenomena such as the spatial localization of dislocation flow into "slip bands"[8](also known as Lüders band) and the temporal fluctuations in stress-strain curves (the Portevin–Le Chatelier effect first reported in the 1920s).[9][1]

Experimental Approach

Although evidence of intermittent flow behavior is long known and studied, it is not until past two decades that a quantitative understanding of the phenomenon is developed with help of novel experimental techniques.

Acoustic emission

Acoustic emission (AE) is used to record the crackling noise from deforming crystals.[10][11] The amplitudes of the acoustic signals can be related to the area swept by the fast-moving dislocations and hence to the energy dissipated during deformation events. The result shows that cracking noise is not smooth, with no specific energy scale. Effect of grain structure for "supercritical" flow has been studied in polycrystalline ice.[12]

Direct mechanical measurement

Recent developments in small scale mechanical testing, with sub-nm resolution in displacement and sub-μN resolution in force, now allow to directly study discrete events in stress and strain. Currently, the most prominent method is a miniaturized compression experiment, where a nanoindenter equipped with a flat indentation tip is used. Equipped with in-situ techniques in combination with Transmission electron microscopy, Scanning electron microscopy, and micro-diffraction methods, this nanomechanical testing method can give us rich detail in nanoscale plasticity instabilities in real time.

One potential concern in nanomechanical measurement is: how fast can the system respond? Can indentation tip remain contact with the sample and track the deformation? Since dislocation velocity is strongly effected by stress, velocity can be many orders different in different systems. Also, multiscale nature of dislocation avalanche event gives dislocation velocity a large range. For example, single dislocations have been shown to move at speeds of ~10 ms−1 in pure Cu, but dislocation groups moved with ~10−6 ms−1 in Cu-0.5%Al. The opposite is found for iron, where dislocation groups are found to move six orders of magnitude faster in a FeSi-alloy than individual dislocations in pure iron.

To resolve this issue, Sparks et al. has designed an experiment to measure first fracture of Si beam and compare with theoretical prediction to determine the respond speed of the system.[13] In addition to regular compression experiments, in-situ electrical contact resistance measurements (ECR) were performed. During these in-situ tests, a constant voltage was applied during the deformation experiment to record current evolution during intermittent plastic flow. Result shows that indentation tip remains contact with the sample throughout experiments, which proves the respond speed is fast enough.

Theoretical analysis and simulations

Avalanche strain distributions have the general form[5]

[math]\displaystyle{ P(s)= C s^{-\tau} exp[-(s/s_0) ^2] }[/math]

where C is a normalization constant, t is a scaling exponent, and s0 is the characteristic strain of the largest avalanches.

Dislocation dynamic simulations have shown that [math]\displaystyle{ \tau }[/math] can be sometimes close to 1.5, but also, many times higher exponents are observed, with values that may even approach 3 in special circumstances.[14][15] While traditional mean-field theory predictions suggest the value of 1.5,[16][17] more advanced mean-field investigations have demonstrated that larger exponents can be caused by non-trivial, but prevalent mechanisms in crystal plasticity that suppress mobile dislocation propulations.[18][19]

Effect of crystal structure on dislocation avalanches

In FCC crystals, scaled velocity shows a main peak in distribution with relatively smooth curve, which is expected from theory except for some disagreement at low velocity.[20] However, in BCC crystal, distribution of scaled velocity is broader and much more dispersed.[21] The result also shows that scaled velocity in BCC is a lot slower than FCC, which is not predicted by mean field theory. A possible explanation this discrepancy is based on different moving speed of edge and screw dislocations in two type of crystals. In FCC crystals, two parts of dislocation move at same velocity, resulting in smooth averaged avalanches profile; whereas in BCC crystals, edge components move fast and escape rapidly, while screw parts propagate slowly, which drag the overall velocity. Based on this explanation, we will also expect a direction dependence of avalanche events in HCP crystals, which currently lack in experimental data.

References

  1. ↑ 1.0 1.1 Lebyodkin, M.A.; Estrin, Y. (2005). "Multifractal analysis of the Portevin–Le Chatelier effect: General approach and application to AlMg and AlMg/Al2O3 alloys". Acta Materialia 53 (12): 3403–3413. doi:10.1016/j.actamat.2005.03.042. Bibcode: 2005AcMat..53.3403L. 
  2. ↑ Wang, G.; Chan, K.C.; Xia, L.; Yu, P.; Shen, J.; Wang, W.H. (2009). "Self-organized intermittent plastic flow in bulk metallic glasses". Acta Materialia 57 (20): 6146–6155. doi:10.1016/j.actamat.2009.08.040. Bibcode: 2009AcMat..57.6146W. 
  3. ↑ Friedman, Nir; Jennings, Andrew T.; Tsekenis, Georgios; Kim, Ju-Young; Tao, Molei et al. (2012-08-30). "Statistics of Dislocation Slip Avalanches in Nanosized Single Crystals Show Tuned Critical Behavior Predicted by a Simple Mean Field Model". Physical Review Letters 109 (9): 095507. doi:10.1103/physrevlett.109.095507. PMID 23002851. Bibcode: 2012PhRvL.109i5507F. 
  4. ↑ Dimiduk, D. M. (2006-05-26). "Scale-Free Intermittent Flow in Crystal Plasticity". Science 312 (5777): 1188–1190. doi:10.1126/science.1123889. PMID 16728635. Bibcode: 2006Sci...312.1188D. 
  5. ↑ 5.0 5.1 Csikor, F. F.; Motz, C.; Weygand, D.; Zaiser, M.; Zapperi, S. (2007-10-12). "Dislocation Avalanches, Strain Bursts, and the Problem of Plastic Forming at the Micrometer Scale". Science 318 (5848): 251–254. doi:10.1126/science.1143719. PMID 17932293. Bibcode: 2007Sci...318..251C. 
  6. ↑ Brinckmann, Steffen; Kim, Ju-Young; Greer, Julia R. (2008-04-17). "Fundamental Differences in Mechanical Behavior between Two Types of Crystals at the Nanoscale". Physical Review Letters 100 (15): 155502. doi:10.1103/physrevlett.100.155502. PMID 18518121. Bibcode: 2008PhRvL.100o5502B. https://scholarworks.unist.ac.kr/handle/201301/7629. 
  7. ↑ Fisher, Daniel S. (1998). "Collective transport in random media: from superconductors to earthquakes". Physics Reports 301 (1–3): 113–150. doi:10.1016/s0370-1573(98)00008-8. Bibcode: 1998PhR...301..113F. 
  8. ↑ Ewing, J. A.; Rosenhain, Walter (1900). "XI. Bakerian lecture.–The crystalline structure of metals". Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 193: 353–375. doi:10.1098/rsta.1900.0011. Bibcode: 1900RSPTA.193..353E. 
  9. ↑ Portevin, A.; Le Chatelier, F. (1923). "Sur un phénomène observé lors de l'essai de traction d'alliages en cours de transformation" (in fr). Comptes rendus de l'Académie des Sciences 176: 507. https://gallica.bnf.fr/ark:/12148/bpt6k31295/f507.image. 
  10. ↑ Miguel, M.-Carmen; Vespignani, Alessandro; Zapperi, Stefano; Weiss, Jérôme; Grasso, Jean-Robert (2001). "Intermittent dislocation flow in viscoplastic deformation". Nature 410 (6829): 667–671. doi:10.1038/35070524. PMID 11287948. Bibcode: 2001Natur.410..667M. 
  11. ↑ Weiss, J. (2003-01-03). "Three-Dimensional Mapping of Dislocation Avalanches: Clustering and Space/Time Coupling". Science 299 (5603): 89–92. doi:10.1126/science.1079312. PMID 12511646. Bibcode: 2003Sci...299...89W. 
  12. ↑ Richeton, Thiebaud; Weiss, Jérôme; Louchet, François (2005-05-08). "Breakdown of avalanche critical behaviour in polycrystalline plasticity". Nature Materials 4 (6): 465–469. doi:10.1038/nmat1393. PMID 15880114. Bibcode: 2005NatMa...4..465R. 
  13. ↑ Sparks, G.; Phani, P. Sudharshan; Hangen, U.; Maaß, R. (2017). "Spatiotemporal slip dynamics during deformation of gold micro-crystals". Acta Materialia 122: 109–119. doi:10.1016/j.actamat.2016.09.026. Bibcode: 2017AcMat.122..109S. 
  14. ↑ Weiss, Jerome; et, al. (2015). "From mild to wild fluctuations in crystal plasticity.". Physical Review Letters 2015 (10): 105504. doi:10.1103/PhysRevLett.114.105504. PMID 25815948. 
  15. ↑ Papanikolaou, S.; et, al. (2012). "Quasi-periodic events in crystal plasticity and the self-organized avalanche oscillator.". Nature 2012 (7421): 517–521. doi:10.1038/nature11568. PMID 23099406. Bibcode: 2012Natur.490..517P. 
  16. ↑ Zaiser, Michael; Moretti, Paolo (2005-08-05). "Fluctuation phenomena in crystal plasticity—a continuum model". Journal of Statistical Mechanics: Theory and Experiment 2005 (8): P08004. doi:10.1088/1742-5468/2005/08/p08004. Bibcode: 2005JSMTE..08..004Z. 
  17. ↑ Zaiser, Michael (2006). "Scale invariance in plastic flow of crystalline solids". Advances in Physics 55 (1–2): 185–245. doi:10.1080/00018730600583514. Bibcode: 2006AdPhy..55..185Z. 
  18. ↑ Weiss, Jerome; et, al (2021). "Fluctuations in crystalline plasticity.". Comptes Rendus Physique 22 (S3): 163–199. doi:10.5802/crphys.51. Bibcode: 2021CRPhy..22S.163W. 
  19. ↑ Song, H; et, al (2019). "Universality Class of Nanocrystal Plasticity: Localization and Self-Organization in Discrete Dislocation Dynamics". Physical Review Letters 122 (17): 178001. doi:10.1103/PhysRevLett.122.178001. PMID 31107061. Bibcode: 2019PhRvL.122q8001S. 
  20. ↑ Papanikolaou, S.; Cui, Yinan; Ghoniem, Nasr (2017). "Avalanches and plastic flow in crystal plasticity: an overview". Modelling and Simulation in Materials Science and Engineering 26: 013001. doi:10.1088/1361-651X/aa97ad. 
  21. ↑ Sparks, G.; Maaß, R. (2018). "Shapes and velocity relaxation of dislocation avalanches in Au and Nb microcrystals". Acta Materialia 152: 86–95. doi:10.1016/j.actamat.2018.04.007. Bibcode: 2018AcMat.152...86S. 

See also



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Dislocation_avalanches&oldid=3277865"