Physics:Electronic speckle pattern interferometry

From HandWiki
ESPI fringes – flat plate rotated about a vertical axis – the fringes represents displacement in the viewing direction; the difference in displacement between fringes is about 0.3 μm.

Electronic speckle pattern interferometry (ESPI),[1] also known as TV holography, is a technique that uses laser light, together with video detection, recording and processing, to visualise static and dynamic displacements of components with optically rough surfaces. The visualisation is in the form of fringes on the image, where each fringe normally represents a displacement of half a wavelength of the light used (i.e. quarter of a micrometre or so).

ESPI can be used for stress and strain measurement, vibration mode analysis and nondestructive testing.[2] ESPI is similar to holographic interferometry in many ways, but there are also significant differences[3] between the two techniques.

How it works

The component under investigation must have an optically rough surface so that when it is illuminated by an expanded laser beam, the image formed is a subjective speckle pattern. The light arriving at a point in the speckled image is scattered from a finite area of the object, and its phase, amplitude and intensity, which are all random, are directly related to the microstructure of that area in the object.

A second light field, known as the reference beam, is derived from the same laser beam and is superimposed on the video camera image (different configurations enable different measurements to be made). The two light fields interfere and the resulting light field has random amplitude, phase and intensity, and is therefore also a speckle pattern. If the object is displaced or deformed, the distance between object and image will change, and hence the phase of the image speckle pattern will change. The relative phases of reference and object beam change, and therefore the intensities of the combined light field changes. However, if the phase change of the object light field is a multiple of 2π, the relative phases of the two light fields will be unchanged, and the intensity of the overall image will also be unchanged.

To visualize this effect, the image and reference beams are combined on a video camera and recorded. When the object has been displaced/deformed, the new image is subtracted point by point from the first image. The resulting image is a speckle pattern with black 'fringes' representing contours of constant 2nπ.

Configurations

Out-of-plane displacement measurement

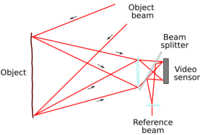
Optical arrangement to obtain out-of-plane ESPI fringes

The reference beam is an expanded beam derived from the laser beam, and is added to the image of the object which is formed on the video camera.

The amplitude of the light at any point in the image is the sum of the light from the object (object beam) and the second beam (reference beam). If the object moves in the direction of viewing, the distance travelled by the object beam changes, its phase changes, and therefore the amplitude of the combined beams changes. When the second speckle pattern is subtracted from the first, fringes are obtained which represent contours of displacement along the viewing direction (out-of-plane displacement). These are not interference fringes, and are sometimes referred to as 'correlation' fringes since they map out areas of the speckle pattern which are more or less correlated. Strictly speaking, the fringes represent purely out-of-plane displacement only if the surface is illuminated normally (this requires a beam splitter to be used to illuminate the object), but the dependence on in-plane movement is relatively small unless the object illumination is well away from the normal direction.

The fringes in the image above are out-of-plane fringes. The plate has been rotated about a vertical axis and the fringes represent contours of constant displacement. The contour interval is about 0.3μm since a He-Ne laser was used in the system. As with many interferometric techniques, it is not possible to identify the zero-order fringe without additional information from the system. That means a rigid body motion of a half wavelength (0.3μm) towards the camera does not change the fringe pattern.

Holographic interferometry provides the same information as out-of-plane ESPI fringes.

Out-of-plane vibration measurement

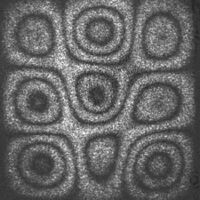
ESPI fringes showing one of the vibration modes of a clamped square plate

The optical arrangement is the same as for out-of-plane displacement above. The object is vibrated at a specific frequency. Those parts of the object which do not move will continue to be speckled. It can be shown that parts of the object which vibrate with amplitudes of nλ/4 have higher speckle contrast than those parts which vibrate at (n+½)λ/4.

This system is simpler to operate than either of the displacement measuring systems, as the fringes are obtained without any recording being required. The vibration mode can be observed in the image from the camera as a variation in speckle contrast rather than as a variation in intensity but it is quite difficult to discern. When the image is high-pass filtered, the variation in contrast is converted to a variation in intensity, and a fringe pattern of the form shown in the diagram is observed where the fringes are clearly visible.

Holographic interferometry can be used in the same way to map out vibration modes.

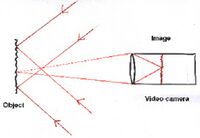
Optical arrangement for viewing in-plane displacement sensitive fringes

In-plane measurement

The object is illuminated by two beams derived from the same laser beam which are incident on the object from opposite sides. When the object is displaced or deformed in the direction normal to the viewing direction (i.e. in it its own plane), the phase of one beam increases, while that of the other decreases, so that the relative phase of the two beams changes. When this change is a multiple of 2π, the speckle pattern coincides with itself (remains the same), while elsewhere it changes.[4] When the subtraction technique described above is used, fringes are obtained which represent in-plane displacement contours.[5]

In-plane displacement gradient measurement

The object is illuminated by two beams derived from the same laser which are incident on the object from the same side but at different angles. When the object is displaced or deformed within its own plane, the relative phases of the two beams change in proportion to the gradient[6] of the in-plane displacement. Again, subtraction of the two images is used to display the fringes.

Holographic interferometry has no equivalent to in-plane measuring[7] ESPI. Acoustic interferometry, among with electromagnetic acoustic transducers, is capable of measure the two polarizations of in-plane vibrations.[8]

See also

References

  1. ↑ Jones R., Wykes C., Holographic and Speckle Interferometry, 1989, Cambridge University Press.
  2. ↑ Shabestari, N. P. (2019). "Fabrication of a simple and easy-to-make piezoelectric actuator and its use as phase shifter in digital speckle pattern interferometry". Journal of Optics 48 (2): 272–282. doi:10.1007/s12596-019-00522-4. 
  3. ↑ Schnars U., Falldorf C., Watson J., Jueptner W., Digital Holography and Wavefront Sensing, Chapter 8, second edition, 2014, Springer.
  4. ↑ Shabestari, N. P. (2019). "Fabrication of a simple and easy-to-make piezoelectric actuator and its use as phase shifter in digital speckle pattern interferometry". Journal of Optics 48 (2): 272–282. doi:10.1007/s12596-019-00522-4. 
  5. ↑ Gasvik K J, Optical Metrology, chapter 6.3, 1987, John Wiley & Sons
  6. ↑ Gasvik K J, Optical Metrology, chapter 6.3, 1987, John Wiley & Sons
  7. ↑ Kreis T, Handbook of Holographic Interferometry, 2004, Wiley-VCH
  8. ↑ In-plane vibrations of a rectangular plate: Plane wave expansion modelling and experiment, A.Arreola-Lucas, J.A.Franco-Villafañe, G.Báez, and R.A.Méndez-Sánchez, Journal of Sound and Vibration Volume 342, (2015), 168–176

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Electronic_speckle_pattern_interferometry&oldid=173105"