Physics:Fatigue limit

From HandWiki
Short description: Maximum stress that won't cause fatigue failure
Representative curves of applied stress vs number of cycles for      steel (showing an endurance limit) and      aluminium (showing no such limit).

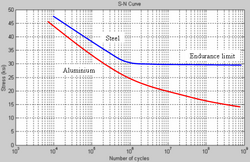
The fatigue limit or endurance limit is the stress level below which an infinite number of loading cycles can be applied to a material without causing fatigue failure.[1] whereas others such as aluminium and copper do not and will eventually fail even from small stress amplitudes. Where materials do not have a distinct limit the term fatigue strength or endurance strength is used and is defined as the maximum value of completely reversed bending stress that a material can withstand for a specified number of cycles without a fatigue failure.[2][3]

Definitions

The ASTM defines fatigue strength, [math]\displaystyle{ S_{N_f} }[/math], as "the value of stress at which failure occurs after [math]\displaystyle{ N_f }[/math] cycles", and fatigue limit, [math]\displaystyle{ S_f }[/math], as "the limiting value of stress at which failure occurs as [math]\displaystyle{ N_f }[/math] becomes very large". ASTM does not define endurance limit, the stress value below which the material will withstand many load cycles,[1] but implies that it is similar to fatigue limit.[4]

Some authors use endurance limit, [math]\displaystyle{ S_e }[/math], for the stress below which failure never occurs, even for an indefinitely large number of loading cycles, as in the case of steel; and fatigue limit or fatigue strength, [math]\displaystyle{ S_f }[/math], for the stress at which failure occurs after a specified number of loading cycles, such as 500 million, as in the case of aluminium.[1][5][6] Other authors do not differentiate between the expressions even if they do differentiate between the two types of materials.[7][8][9]

Typical values

Typical values of the limit ([math]\displaystyle{ S_e }[/math]) for steels are one half the ultimate tensile strength, to a maximum of 290 MPa (42 ksi). For iron, aluminium, and copper alloys, [math]\displaystyle{ S_e }[/math] is typically 0.4 times the ultimate tensile strength. Maximum typical values for irons are 170 MPa (24 ksi), aluminums 130 MPa (19 ksi), and coppers 97 MPa (14 ksi).[10] Note that these values are for smooth "un-notched" test specimens. The endurance limit for notched specimens (and thus for many practical design situations) is significantly lower.

For polymeric materials, the fatigue limit has been shown to reflect the intrinsic strength of the covalent bonds in polymer chains that must be ruptured in order to extend a crack. So long as other thermo chemical processes do not break the polymer chain (i.e. ageing or ozone attack), a polymer may operate indefinitely without crack growth when loads are kept below the intrinsic strength.[11][12]

The concept of fatigue limit, and thus standards based on a fatigue limit such as ISO 281:2007 rolling bearing lifetime prediction, remains controversial, at least in the US.[13][14]

Modifying factors of fatigue limit

The fatigue limit of a machine component, Se, is influenced by a series of elements named modifying factors. Some of these factors are listed below.

Surface factor

The surface modifying factor, [math]\displaystyle{ k_S }[/math], is related to both the tensile strength, [math]\displaystyle{ S_{ut} }[/math], of the material and the surface finish of the machine component.

[math]\displaystyle{ k_{S}=aS_{ut}^b }[/math]

Where factor a and exponent b present in the equation are related to the surface finish.

Gradient factor

Besides taking into account the surface finish, it is also important to consider the size gradient factor [math]\displaystyle{ k_{G} }[/math]. When it comes to bending and torsional loading, the gradient factor is also taken into consideration.

Load factor

Load modifying factor can be identified as.

[math]\displaystyle{ k_{L}=0.85 }[/math] for axial

[math]\displaystyle{ k_{L}=1 }[/math] for bending

[math]\displaystyle{ k_{L}=0.59 }[/math] for pure tension

Temperature factor

The temperature factor is calculated as

[math]\displaystyle{ k_{T}= \frac{S_{o}}{S_{r}} }[/math]

[math]\displaystyle{ S_o }[/math] is tensile strength at operating temperature

[math]\displaystyle{ S_{r} }[/math] is tensile strength at room temperature

Reliability factor

We can calculate the reliability factor using the equation

[math]\displaystyle{ k_{R}=1-0.08Z_{a} }[/math]

[math]\displaystyle{ z_{a}=0 }[/math] for 50% reliability

[math]\displaystyle{ z_{a}=1.288 }[/math] for 90% reliability

[math]\displaystyle{ z_{a}=1.645 }[/math] for 95% reliability

[math]\displaystyle{ z_{a}=2.326 }[/math] for 99% reliability

History

The concept of endurance limit was introduced in 1870 by August Wöhler.[15] However, recent research suggests that endurance limits do not exist for metallic materials, that if enough stress cycles are performed, even the smallest stress will eventually produce fatigue failure.[6][16]

See also

  • Fatigue (material)
  • Smith fatigue strength diagram (de), a diagram by British mechanical engineer James Henry Smith (de)

References

  1. ↑ 1.0 1.1 1.2 Beer, Ferdinand P.; E. Russell Johnston Jr. (1992). Metal Fatigue and Endurance (2 ed.). McGraw-Hill, Inc.. p. 51. ISBN 978-0-07-837340-4. http://www.roymech.co.uk/Useful_Tables/Fatigue/Fatigue.html. Retrieved 2008-04-18. 
  2. ↑ Jastrzebski, D. (1959). Nature and Properties of Engineering Materials (Wiley International ed.). John Wiley & Sons, Inc. 
  3. ↑ Suresh, S. (2004). Fatigue of Materials. Cambridge University Press. ISBN 978-0-521-57046-6. 
  4. ↑ Stephens, Ralph I. (2001). Metal Fatigue in Engineering (2nd ed.). John Wiley & Sons, Inc.. p. 69. ISBN 978-0-471-51059-8. https://archive.org/details/metalfatigueengi00step. 
  5. ↑ Budynas, Richard G. (1999). Advanced Strength and Applied Stress Analysis (2nd ed.). McGraw-Hill, Inc.. pp. 532–533. ISBN 978-0-07-008985-3. https://archive.org/details/advancedstrength00budy. 
  6. ↑ 6.0 6.1 Askeland, Donald R.; Pradeep P. Phule (2003). The Science and Engineering of Materials (4th ed.). Brooks/Cole. p. 248. ISBN 978-0-534-95373-7. 
  7. ↑ Hibbeler, R. C. (2003). Mechanics of Materials (5th ed.). Pearson Education, Inc.. p. 110. ISBN 978-0-13-008181-0. 
  8. ↑ Dowling, Norman E. (1998). Mechanical Behavior of Materials (2nd ed.). Printice-Hall, Inc.. p. 365. ISBN 978-0-13-905720-5. 
  9. ↑ Barber, J. R. (2001). Intermediate Mechanics of Materials. McGraw-Hill. p. 65. ISBN 978-0-07-232519-5. 
  10. ↑ Cite error: Invalid <ref> tag; no text was provided for refs named MFandE
  11. ↑ Lake, G. J.; P. B. Lindley (1965). "The mechanical fatigue limit for rubber". Journal of Applied Polymer Science 9 (4): 1233–1251. doi:10.1002/app.1965.070090405. 
  12. ↑ Lake, G. J.; A. G. Thomas (1967). "The strength of highly elastic materials". Proceedings of the Royal Society of London A: Mathematical and Physical Sciences 300 (1460): 108–119. doi:10.1098/rspa.1967.0160. Bibcode: 1967RSPSA.300..108L. 
  13. ↑ Erwin V. Zaretsky (August 2010). "In search of a fatigue limit: A critique of ISO standard 281:2007". Tribology & Lubrication Technology: 30–40. http://www.stle.org/assets/document/8-10_tlt_commentary_ISO_Standard_281_2007_Part_II.pdf. 
  14. ↑ "ISO 281:2007 bearing life standard – and the answer is?". Tribology & Lubrication Technology: 34–43. July 2010. https://www.stle.org/assets/document/tlt_July_cover_story_article.pdf. 
  15. ↑ W. Schutz (1996). A history of fatigue. Engineering Fracture Mechanics 54: 263-300. DOI
  16. ↑ Bathias, C. (1999). "There is no infinite fatigue life in metallic materials". Fatigue & Fracture of Engineering Materials & Structures 22 (7): 559–565. doi:10.1046/j.1460-2695.1999.00183.x. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Fatigue_limit&oldid=3279570"