Physics:Fréedericksz transition

Short description: Phase transition of liquid crystals

The Fréedericksz transition is a phase transition in liquid crystals produced when a sufficiently strong electric or magnetic field is applied to a liquid crystal in an undistorted state. Below a certain field threshold the director remains undistorted. As the field value is gradually increased from this threshold, the director begins to twist until it is aligned with the field. In this fashion the Fréedericksz transition can occur in three different configurations known as the twist, bend, and splay geometries. The phase transition was first observed by Fréedericksz and Repiewa in 1927. In this first experiment of theirs, one of the walls of the cell was concave so as to produce a variation in thickness along the cell. The phase transition is named in honor of the Russian physicist Vsevolod Frederiks.

Derivation

Twist geometry

A diagram showing the twist geometry, where [math]\displaystyle{ E_t }[/math] is the threshold electric field.

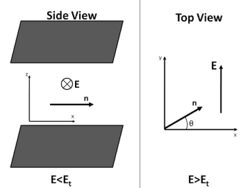
If a nematic liquid crystal that is confined between two parallel plates that induce a planar anchoring is placed in a sufficiently high constant electric field then the director will be distorted. If under zero field the director aligns along the x-axis then upon application of an electric field along the y-axis the director will be given by:

[math]\displaystyle{ \mathbf{\hat{n}}=n_x\mathbf{\hat{x}}+n_y\mathbf{\hat{y}} }[/math]

[math]\displaystyle{ n_x=\cos{\theta(z)} }[/math]

[math]\displaystyle{ n_y=\sin{\theta(z)} }[/math]

Under this arrangement the distortion free energy density becomes:

[math]\displaystyle{ \mathcal{F}_{d}=\frac{1}{2}K_2\left(\frac{d\theta}{dz}\right)^2 }[/math]

The total energy per unit volume stored in the distortion and the electric field is given by:

[math]\displaystyle{ U=\frac{1}{2}K_2\left(\frac{d\theta}{dz}\right)^2-\frac{1}{2}\epsilon_0\Delta\chi_eE^2\sin^2{\theta} }[/math]

The free energy per unit area is then:

[math]\displaystyle{ F_A=\int_0^d\frac{1}{2}K_2\left(\frac{d\theta}{dz}\right)^2-\frac{1}{2}\epsilon_0\Delta\chi_eE^2\sin^2{\theta}\,dz \, }[/math]

Minimizing this using calculus of variations gives:

[math]\displaystyle{ \left(\frac{\partial U}{\partial \theta}\right)-\frac{d}{dz}\left(\frac{\partial U}{\partial\left(\frac{d\theta}{dz}\right)}\right)=0 }[/math]

[math]\displaystyle{ K_2\left(\frac{d^2\theta}{dz^2}\right)+\epsilon_0\Delta\chi_eE^2\sin{\theta}\cos{\theta}=0 }[/math]

Rewriting this in terms of [math]\displaystyle{ \zeta=\frac{z}{d} }[/math] and [math]\displaystyle{ \xi_d=d^{-1}\sqrt{\frac{K_2}{\epsilon_0\Delta\chi_eE^2}} }[/math] where [math]\displaystyle{ d }[/math] is the separation distance between the two plates results in the equation simplifying to:

[math]\displaystyle{ \xi_d^2\left(\frac{d^2\theta}{d\zeta^2}\right)+\sin{\theta}\cos{\theta}=0 }[/math]

By multiplying both sides of the differential equation by [math]\displaystyle{ \frac{d\theta}{d\zeta} }[/math] this equation can be simplified further as follows:

[math]\displaystyle{ \frac{d\theta}{d\zeta}\xi_d^2\left(\frac{d^2\theta}{d\zeta^2}\right)+\frac{d\theta}{d\zeta}\sin{\theta}\cos{\theta}=\frac{1}{2}\xi_d^2\frac{d}{d\zeta}\left(\left(\frac{d\theta}{d\zeta}\right)^2\right)+\frac{1}{2}\frac{d}{d\zeta}\left ( \sin^2{\theta}\right)=0 }[/math]

[math]\displaystyle{ \int\frac{1}{2}\xi_d^2\frac{d}{d\zeta}\left(\left(\frac{d\theta}{d\zeta}\right)^2\right)+\frac{1}{2}\frac{d}{d\zeta}\left ( \sin^2{\theta}\right)\,d\zeta \,=0 }[/math]

[math]\displaystyle{ \frac{d\theta}{d\zeta}=\frac{1}{\xi_d}\sqrt{\sin^2{\theta_m}-\sin^2{\theta}} }[/math]

The value [math]\displaystyle{ \theta_m }[/math] is the value of [math]\displaystyle{ \theta }[/math] when [math]\displaystyle{ \zeta=1/2 }[/math]. Substituting [math]\displaystyle{ k=\sin{\theta_m} }[/math] and [math]\displaystyle{ t=\frac{\sin{\theta}}{\sin{\theta_m}} }[/math] into the equation above and integrating with respect to [math]\displaystyle{ t }[/math] from 0 to 1 gives:

[math]\displaystyle{ \int_0^1\frac{1}{\sqrt{(1-t^2)(1-k^2t^2)}}\,dt \,\equiv K(k)=\frac{1}{2\xi_d} }[/math]

The value K(k) is the complete elliptic integral of the first kind. By noting that [math]\displaystyle{ K(0)=\frac{\pi}{2} }[/math] one finally obtains the threshold electric field [math]\displaystyle{ E_t }[/math].

[math]\displaystyle{ E_t=\frac{\pi}{d}\sqrt{\frac{K_2}{\epsilon_0\Delta\chi_e}} }[/math]

As a result, by measuring the threshold electric field one can effectively measure the twist Frank constant so long as the anisotropy in the electric susceptibility and plate separation is known.

References

• Collings, Peter J.; Hird, Michael (1997). Introduction to Liquid Crystals: Chemistry and Physics. Taylor & Francis Ltd.. ISBN 0-7484-0643-3. https://archive.org/details/introductiontoli0000coll. 
• de Gennes, Pierre-Gilles; Prost, J. (10 August 1995). The Physics of Liquid Crystals (2nd ed.). Oxford University Press. ISBN 0-19-851785-8. 
• Fréedericksz, V.; Repiewa, A. (1927). "Theoretisches und Experimentelles zur Frage nach der Natur der anisotropen Flüssigkeiten". Zeitschrift für Physik 42 (7): 532–546. doi:10.1007/BF01397711. Bibcode: 1927ZPhy...42..532F. 
• Fréedericksz, V.; Zolina, V. (1933). "Forces causing the orientation of an anisotropic liquid". Trans. Faraday Soc. 29 (140): 919–930. doi:10.1039/TF9332900919. 
• Priestley, E. B.; Wojtowicz, Peter J.; Sheng, Ping (1975). Introduction to Liquid Crystals. Plenum Press. ISBN 0-306-30858-4. 
• Zöcher, H. (1933). "The effect of a magnetic field on the nematic state". Transactions of the Faraday Society 29 (140): 945–957. doi:10.1039/TF9332900945.