Physics:Geopotential
Geopotential (symbol W) is the potential of the Earth's gravity field. It has SI units of square metre per square seconds (m2/s2). For convenience it is often defined as the negative of the potential energy per unit mass, so that the gravity vector is obtained as the gradient of the geopotential, without the negation. In addition to the actual potential (the geopotential), a theoretical normal potential (symbol U) and their difference, the disturbing potential (T = W − U), can also be defined.
Concepts
For geophysical applications, gravity is distinguished from gravitation. Gravity is defined as the resultant force of gravitation and the centrifugal force caused by the Earth's rotation. Likewise, the respective scalar potentials, gravitational potential and centrifugal potential, can be added to form an effective potential called the geopotential, . The surfaces of constant geopotential or isosurfaces of the geopotential are called equigeopotential surfaces (sometimes abbreviated as geop),[1] also known as geopotential level surfaces, equipotential surfaces, or simply level surfaces.[2]
Global mean sea surface is close to one equigeopotential called the geoid.[3] How the gravitational force and the centrifugal force add up to a force orthogonal to the geoid is illustrated in the figure (not to scale). At latitude 50 deg the off-set between the gravitational force (red line in the figure) and the local vertical (green line in the figure) is in fact 0.098 deg. For a mass point (atmosphere) in motion the centrifugal force no more matches the gravitational and the vector sum is not exactly orthogonal to the Earth surface. This is the cause of the coriolis effect for atmospheric motion.
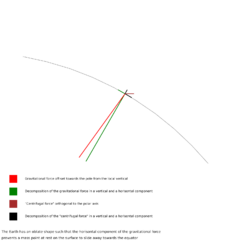
The geoid is a gently undulating surface due to the irregular mass distribution inside the Earth; it may be approximated however by an ellipsoid of revolution called the reference ellipsoid. The currently most widely used reference ellipsoid, that of the Geodetic Reference System 1980 (GRS80), approximates the geoid to within a little over ±100 m. One can construct a simple model geopotential that has as one of its equipotential surfaces this reference ellipsoid, with the same model potential as the true potential of the geoid; this model is called a normal potential. The difference is called the disturbing potential. Many observable quantities of the gravity field, such as gravity anomalies and deflections of the vertical (plumb-line), can be expressed in this disturbing potential.
Background
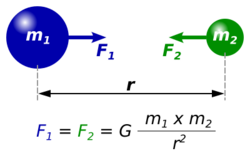
Newton's law of universal gravitation states that the gravitational force F acting between two point masses m1 and m2 with centre of mass separation r is given by where G is the gravitational constant, and r̂ is the radial unit vector. For a non-pointlike object of continuous mass distribution, each mass element dm can be treated as mass distributed over a small volume, so the volume integral over the extent of object 2 gives
-
()
with corresponding gravitational potential
-
()
where ρ2 = ρ(x, y, z) is the mass density at the volume element and of the direction from the volume element to point mass 1. [clarification needed] is the gravitational potential energy per unit mass.
Earth's gravity field can be derived from a gravity potential (geopotential) field as follows: which expresses the gravity acceleration vector as the gradient of , the potential of gravity. The vector triad is the orthonormal set of base vectors in space, pointing along the coordinate axes. Here, , and are geocentric coordinates.
Formulation
Both gravity and its potential contain a contribution from the centrifugal pseudo-force due to the Earth's rotation. We can write where is the potential of the gravitational field, that of the gravity field, and that of the centrifugal field.
Centrifugal potential
The centrifugal force per unit mass—i.e., acceleration—is given by where is the vector pointing to the point considered straight from the Earth's rotational axis. It can be shown that this pseudo-force field, in a reference frame co-rotating with the Earth, has a potential associated with it in terms of Earth's rotation rate ω: This can be verified by taking the gradient () operator of this expression.
The centrifugal potential can also be expressed in terms of spherical latitude φ and geocentric radius r: or in terms of perpendicular distance ρ to the axis or rotation: Note that the spherical latitude is measured from the equator, not from the pole.
Normal potential
The Earth is approximately an ellipsoid. So, it is accurate to approximate the geopotential by a field that has the Earth reference ellipsoid as one of its equipotential surfaces.
Like the actual geopotential field W, the normal field U (not to be confused with the potential energy, also U) is constructed as a two-part sum: where is the normal gravitational potential, and is the centrifugal potential.
A closed-form exact expression exists in terms of ellipsoidal-harmonic coordinates (not to be confused with geodetic coordinates).[4] It can also be expressed as a series expansion in terms of spherical coordinates; truncating the series results in:[4] where a is semi-major axis, and J2 is the second dynamic form factor.[4]
The most recent Earth reference ellipsoid is GRS80, or Geodetic Reference System 1980, which the Global Positioning System uses as its reference. Its geometric parameters are: semi-major axis a = 6378137.0 m, and flattening f = 1/298.257222101. If we also require that the enclosed mass M is equal to the known mass of the Earth (including atmosphere), as involved in the standard gravitational parameter, GM = 3986005×108 m3/s2, we obtain for the potential at the reference ellipsoid:
Obviously, this value depends on the assumption that the potential goes asymptotically to zero at infinity (), as is common in physics. For practical purposes it makes more sense to choose the zero point of normal gravity to be that of the reference ellipsoid, and refer the potentials of other points to this.
Disturbing potential
Once a clean, smooth geopotential field has been constructed, matching the known GRS80 reference ellipsoid with an equipotential surface (we call such a field a normal potential), it can be subtracted from the true (measured) potential of the real Earth. The result is defined as T, the disturbing potential:
The disturbing potential T is numerically a much smaller than U or W and captures the detailed, complex variations of the true gravity field of the actually existing Earth from point to point, as distinguished from the overall global trend captured by the smooth mathematical ellipsoid of the normal potential.
Geopotential number
In practical terrestrial work, e.g., levelling, an alternative version of the geopotential is used called geopotential number , which are reckoned from the geoid upward: where is the geopotential of the geoid.
Simple case: nonrotating symmetric sphere
In the special case of a sphere with a spherically symmetric mass density, ρ = ρ(s); i.e., density depends only on the radial distance
These integrals can be evaluated analytically. This is the shell theorem saying that in this case:
-
()
with corresponding potential
-
()
where is the total mass of the sphere.
For the purpose of satellite orbital mechanics, the geopotential is typically described by a series expansion into spherical harmonics (spectral representation). In this context the geopotential is taken as the potential of the gravitational field of the Earth, that is, leaving out the centrifugal potential.
Solving for geopotential in the simple case of a nonrotating sphere, in units of [m2/s2] or [J/kg]:[5]
Integrate to get where
- G = 6.673×10−11 Nm2/kg2 is the gravitational constant,
- m = 5.975×1024 kg is the mass of the earth,
- a = 6.378×106 m is the average radius of the earth,
- z is the geometric height in meters.
See also
- Dynamic height
- Geoid
- Geopotential height
- Geopotential model
- Normal gravity
- Physical geodesy
References
- ↑ Hooijberg, M. (2007). Geometrical Geodesy: Using Information and Computer Technology. Springer Berlin Heidelberg. p. 9. ISBN 978-3-540-68225-7. https://books.google.com/books?id=NJhdIuyrWmoC&pg=PA9. Retrieved 2023-09-11.
- ↑ "Geopotential". https://glossary.ametsoc.org/wiki/Geopotential_surface.
- ↑ Heiskanen, Weikko Aleksanteri; Moritz, Helmut (1967). Physical Geodesy. W.H. Freeman. ISBN 0-7167-0233-9.
- ↑ 4.0 4.1 4.2 Torge, Geodesy. 3rd ed. 2001.
- ↑ Holton, James R. (2004). An Introduction to Dynamic Meteorology (4th ed.). Burlington: Elsevier. ISBN 0-12-354015-1.
 |
