Physics:Grain growth

In materials science, grain growth is the increase in size of grains (crystallites) in a material at high temperature. This occurs when recovery and recrystallisation are complete and further reduction in the internal energy can only be achieved by reducing the total area of grain boundary. The term is commonly used in metallurgy but is also used in reference to ceramics and minerals. The behaviors of grain growth is analogous to the coarsening behaviors of grains, which implied that both of grain growth and coarsening may be dominated by the same physical mechanism.

Importance of grain growth

The practical performances of polycrystalline materials are strongly affected by the formed microstructure inside, which is mostly dominated by grain growth behaviors. For example, most materials exhibit the Hall–Petch effect at room-temperature and so display a higher yield stress when the grain size is reduced (assuming abnormal grain growth has not taken place). At high temperatures the opposite is true since the open, disordered nature of grain boundaries means that vacancies can diffuse more rapidly down boundaries leading to more rapid Coble creep. Since boundaries are regions of high energy they make excellent sites for the nucleation of precipitates and other second-phases e.g. Mg–Si–Cu phases in some aluminium alloys or martensite platlets in steel. Depending on the second phase in question this may have positive or negative effects.

Rules of grain growth

Grain growth has long been studied primarily by the examination of sectioned, polished and etched samples under the optical microscope. Although such methods enabled the collection of a great deal of empirical evidence, particularly with regard to factors such as temperature or composition, the lack of crystallographic information limited the development of an understanding of the fundamental physics. Nevertheless, the following became well-established features of grain growth:

1. Grain growth occurs by the movement of grain boundaries and also by coalescence (i.e. like water droplets)
2. Grain growth competition between Ordered coalescence and the movement of grain boundaries
3. Boundary movement may be discontinuous and the direction of motion may change suddenly during abnormal grain growth.
4. One grain may grow into another grain whilst being consumed from the other side
5. The rate of consumption often increases when the grain is nearly consumed
6. A curved boundary typically migrates towards its centre of curvature

Classical driving force

The boundary between one grain and its neighbour (grain boundary) is a defect in the crystal structure and so it is associated with a certain amount of energy. As a result, there is a thermodynamic driving force for the total area of boundary to be reduced. If the grain size increases, accompanied by a reduction in the actual number of grains per volume, then the total area of grain boundary will be reduced.

In the classic theory, the local velocity of a grain boundary at any point is proportional to the local curvature of the grain boundary, i.e.:

[math]\displaystyle{ v=M \sigma \kappa }[/math],

where [math]\displaystyle{ v }[/math] is the velocity of grain boundary, [math]\displaystyle{ M }[/math] is grain boundary mobility (generally depends on orientation of two grains), [math]\displaystyle{ \sigma }[/math] is the grain boundary energy and [math]\displaystyle{ \kappa }[/math] is the sum of the two principal surface curvatures. For example, shrinkage velocity of a spherical grain embedded inside another grain is

[math]\displaystyle{ v= M \sigma \frac{2}{R} }[/math],

where [math]\displaystyle{ R }[/math] is radius of the sphere. This driving pressure is very similar in nature to the Laplace pressure that occurs in foams.

In comparison to phase transformations the energy available to drive grain growth is very low and so it tends to occur at much slower rates and is easily slowed by the presence of second phase particles or solute atoms in the structure.

Recently, in contrast to the classic linear relation between grain boundary velocity and curvature, grain boundary velocity and curvature are observed to be not correlated in Ni polycrystals, which conflicting results has been revealed and be theoretically interpreted by a general model of grain boundary (GB) migration in the previous literature. According to the general GB migration model, the classical linear relation can only be used in a specical case.

A general theory of grain growth

Development of theoretical models describing grain growth is an active field of research. Many models have been proposed for grain growth, but no theory has yet been put forth that has been independently validated to apply across the full range of conditions and many questions remain open. By no means is the following a comprehensive review. One recent theory of grain growth posits that normal grain growth only occurs in the polycrystalline systems with grain boundaries which have undergone roughening transitions, and abnormal and/or stagnant grain growth can only occur in the polycrystalline systems with non-zero GB (grain boundary) step free energy of grains. Other models explaining grain coarsening assert that disconnections are responsible for the motion of grain boundaries, and provide limited experimental evidence suggesting that they govern grain boundary migration and grain growth behavior. Other models have indicated that triple junctions play an important role in determining the grain growth behavior in many systems.

Ideal grain growth

thumb|300px|Computer Simulation of Grain Growth in 3D using phase field model. Click to see the animation. Ideal grain growth is a special case of normal grain growth where boundary motion is driven only by local curvature of the grain boundary. It results in the reduction of the total amount of grain boundary surface area i.e. total energy of the system. Additional contributions to the driving force by e.g. elastic strains or temperature gradients are neglected. If it holds that the rate of growth is proportional to the driving force and that the driving force is proportional to the total amount of grain boundary energy, then it can be shown that the time t required to reach a given grain size is approximated by the equation

[math]\displaystyle{ d^2 - {d_0}^2 = kt \,\! }[/math]

where d₀ is the initial grain size, d is the final grain size and k is a temperature dependent constant given by an exponential law:

[math]\displaystyle{ k = k_0 \exp \left ( \frac{-Q}{RT} \right ) \,\! }[/math]

where k₀ is a constant, T is the absolute temperature and Q is the activation energy for boundary mobility. Theoretically, the activation energy for boundary mobility should equal that for self-diffusion but this is often found not to be the case.

In general these equations are found to hold for ultra-high purity materials but rapidly fail when even tiny concentrations of solute are introduced.

Self-similarity

Click to see the animation. Geometry of a single growing grain is changing during grain growth. This is extracted from a large scale phase-field simulation. Here surfaces are "grain boundaries", edges are "triple junctions" and corners are vertexes or higher-order junctions. For more information please see.

An old-standing topic in grain growth is the evolution of the grains size distribution. Inspired by the work of Lifshitz and Slyozov on Ostwald ripening, Hillert has suggested that in a normal grain growth process the size distribution function must converge to a self-similar solution, i.e. it becomes invariant when the grain size is scaled with a characteristic length of the system [math]\displaystyle{ R_{cr} }[/math]that is proportional to the average grain size [math]\displaystyle{ \langle R \rangle }[/math].

Several simulation studies, however, have shown that the size distribution deviates from the Hillert's self-similar solution. Hence a search for a new possible self-similar solution was initiated that indeed led to a new class of self-similar distribution functions. Large-scale phase field simulations have shown that there is indeed a self-similar behavior possible within the new distribution functions. It was shown that the origin of the deviation from Hillert's distribution is indeed the geometry of grains specially when they are shrinking.

Normal vs abnormal

Distinction between continuous (normal) grain growth, where all grains grow at roughly the same rate, and discontinuous (abnormal) grain growth, where one grain grows at a much greater rate than its neighbours.

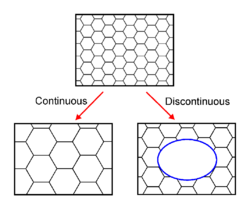
In common with recovery and recrystallisation, growth phenomena can be separated into continuous and discontinuous mechanisms. In the former the microstructure evolves from state A to B (in this case the grains get larger) in a uniform manner. In the latter, the changes occur heterogeneously and specific transformed and untransformed regions may be identified. Abnormal or discontinuous grain growth is characterised by a subset of grains growing at a high rate and at the expense of their neighbours and tends to result in a microstructure dominated by a few very large grains. In order for this to occur the subset of grains must possess some advantage over their competitors such as a high grain boundary energy, locally high grain boundary mobility, favourable texture or lower local second-phase particle density.

Factors hindering growth

If there are additional factors preventing boundary movement, such as Zener pinning by particles, then the grain size may be restricted to a much lower value than might otherwise be expected. This is an important industrial mechanism in preventing the softening of materials at high temperature.

Inhibition

Certain materials especially refractories which are processed at high temperatures end up with excessively large grain size and poor mechanical properties at room temperature. To mitigate this problem in a common sintering procedure, a variety of dopants are often used to inhibit grain growth.

References

• F. J. Humphreys and M. Hatherly (1995); Recrystallization and related annealing phenomena, Elsevier