Physics:Hosford yield criterion

The Hosford yield criterion is a function that is used to determine whether a material has undergone plastic yielding under the action of stress.

Hosford yield criterion for isotropic plasticity

The plane stress, isotropic, Hosford yield surface for three values of n

The Hosford yield criterion for isotropic materials is a generalization of the von Mises yield criterion. It has the form

$\frac{1}{2}|{\sigma }_2-{\sigma }_3{|}^n+\frac{1}{2}|{\sigma }_3-{\sigma }_1{|}^n+\frac{1}{2}|{\sigma }_1-{\sigma }_2{|}^n={\sigma }_y^n$

where ${\sigma }_i$, i=1,2,3 are the principal stresses, $n$ is a material-dependent exponent and ${\sigma }_y$ is the yield stress in uniaxial tension/compression.

Alternatively, the yield criterion may be written as

${\sigma }_y={(\frac{1}{2}|{\sigma }_2-{\sigma }_3{|}^n+\frac{1}{2}|{\sigma }_3-{\sigma }_1{|}^n+\frac{1}{2}|{\sigma }_1-{\sigma }_2{|}^n)}^{1/n}.$

This expression has the form of an L^p norm which is defined as

$\Vert x{\Vert }_p={(|x_1{|}^p+|x_2{|}^p+\cdots +|x_n{|}^p)}^{1/p}.$

When $p=\mathrm{\infty }$, the we get the L^∞ norm,

$\Vert x{\Vert }_{\mathrm{\infty }}=\max \{|x_1|,|x_2|,\dots ,|x_n|\}$. Comparing this with the Hosford criterion

indicates that if n = ∞, we have

$({\sigma }_y{)}_{n\to \mathrm{\infty }}=\max (|{\sigma }_2-{\sigma }_3|,|{\sigma }_3-{\sigma }_1|,|{\sigma }_1-{\sigma }_2|).$

This is identical to the Tresca yield criterion.

Therefore, when n = 1 or n goes to infinity the Hosford criterion reduces to the Tresca yield criterion. When n = 2 the Hosford criterion reduces to the von Mises yield criterion.

Note that the exponent n does not need to be an integer.

Hosford yield criterion for plane stress

For the practically important situation of plane stress, the Hosford yield criterion takes the form

$\frac{1}{2}(|{\sigma }_1{|}^n+|{\sigma }_2{|}^n)+\frac{1}{2}|{\sigma }_1-{\sigma }_2{|}^n={\sigma }_y^n$

A plot of the yield locus in plane stress for various values of the exponent $n\ge 1$ is shown in the adjacent figure.

Logan-Hosford yield criterion for anisotropic plasticity

The plane stress, anisotropic, Hosford yield surface for four values of n and R=2.0

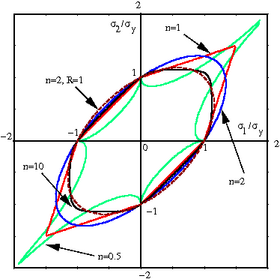
The Logan-Hosford yield criterion for anisotropic plasticity is similar to Hill's generalized yield criterion and has the form

$F|{\sigma }_2-{\sigma }_3{|}^n+G|{\sigma }_3-{\sigma }_1{|}^n+H|{\sigma }_1-{\sigma }_2{|}^n=1$

where F,G,H are constants, ${\sigma }_i$ are the principal stresses, and the exponent n depends on the type of crystal (bcc, fcc, hcp, etc.) and has a value much greater than 2. Accepted values of $n$ are 6 for bcc materials and 8 for fcc materials.

Though the form is similar to Hill's generalized yield criterion, the exponent n is independent of the R-value unlike the Hill's criterion.

Logan-Hosford criterion in plane stress

Under plane stress conditions, the Logan-Hosford criterion can be expressed as

$\frac{1}{1+R}(|{\sigma }_1{|}^n+|{\sigma }_2{|}^n)+\frac{R}{1+R}|{\sigma }_1-{\sigma }_2{|}^n={\sigma }_y^n$

where $R$ is the R-value and ${\sigma }_y$ is the yield stress in uniaxial tension/compression. For a derivation of this relation see Hill's yield criteria for plane stress. A plot of the yield locus for the anisotropic Hosford criterion is shown in the adjacent figure. For values of $n$ that are less than 2, the yield locus exhibits corners and such values are not recommended.

See also

• Yield surface
• Yield (engineering)
• Plasticity
• Stress